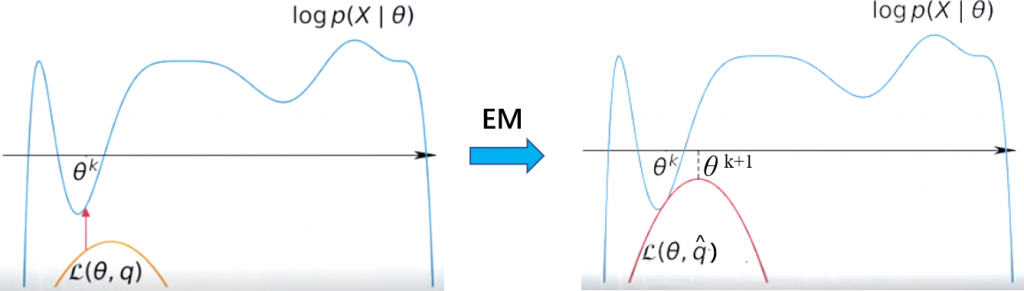
EM算法
EM算法主要用于求解概率密度函数的参数最大似然估计,它的关键是在概率模型中引入隐变量,从而简化概率模型的结构。假设\vec{\theta}为需要求解的参数,\vec{t}为引入的隐变量,我们可以先任意给定一个关于\vec{t}的分布q(\vec{t}),定义\mathcal f(X,\vec{\theta})=\ln p(X|\vec{\theta}),则最大似然估计的求解可变为:
\large{\argmax _{\vec{\theta}} \mathcal f(X,\vec{\theta})=\argmax _{\vec{\theta}} \ln p(X | \vec{\theta})= \argmax _{\vec{\theta}} \int_{\vec{t}} \ln p(X | \vec{\theta})q(\vec{t})d_{\vec{t}}}
其中X表示样本集合,继续对上式进行转换可得:
\large{\begin{aligned} \mathcal f(X, \vec{\theta}) &= \int_{\vec{t}} \ln p(X | \vec{\theta})q(\vec{t})d_{\vec{t}} = \int_{\vec{t}} \ln\frac{p(X,\vec{t} | \vec{\theta})} {p( \vec{t} | X,\vec{\theta})} q(\vec{t})d_{\vec{t}} = \int_{\vec{t}} q(\vec{t})\ln \frac{p(X,\vec{t} | \vec{\theta})q(\vec{t})} {p( \vec{t} | X,\vec{\theta})q(\vec{t})} d_{\vec{t}} \\ &= \underbrace{\int_{\vec{t}} q(\vec{t})\ln \frac{p(X,\vec{t} | \vec{\theta})} {q(\vec{t})} d_{\vec{t}}}_{\large \text { define this to }\mathcal{L}(X,\vec{\theta},q)}+ \underbrace{\int_{\vec{t}} q(\vec{t})\ln \frac{q(\vec{t})} {p( \vec{t} | X,\vec{\theta})} d_{\vec{t}}}_{\large \text { KL divergence }} \end{aligned}}
KL divergence是衡量两个分布的距离的指标,容易看出
KL\left(q(\vec t) \| p(\vec t|X,\vec \theta)\right)=E_q\left[\ln\frac{q(\vec{t})}{p(\vec{t} | X, \vec{\theta})}\right]=\underbrace{-E_q\left[\ln\frac{p(\vec{t} | X, \vec{\theta})}{q(\vec{t})}\right]\ge -\ln E_q\left[\frac{p(\vec{t} | X, \vec{\theta})}{q(\vec{t})}\right]}_{\large \text{Jensen's inequality}}=-\ln\int_{\vec t}\frac{p(\vec{t} | X, \vec{\theta})}{q(\vec{t})}q(\vec t)d_{\vec t}=0
当且仅当两个分布相同时它们的KL divergence为0,即上述不等式中的等号成立。因此有不等式
\tag{1}\mathcal f(X,\vec \theta)= \mathcal{L}(X, \vec{\theta}, q)+KL\left(q(\vec t) \| p(\vec t|X,\vec \theta)\right)\ge \mathcal{L}(X,{\vec{\theta}},q)
对所有的分布q(\vec t)均成立。若在\vec{\theta}的取值范围内任取一个值\hat{\vec{\theta}},并且记分布\hat{q}(\vec t)为p(\vec t | X, \hat{\vec \theta}),则根据公式(1)有
\tag{2}\mathcal f(X,\hat{\vec\theta}) = \mathcal{L}(X, \hat{\vec\theta}, \hat q)+KL\left(\hat q(\vec t) \| p(\vec t|X,\hat{\vec\theta})\right)=\mathcal{L}(X, \hat{\vec{\theta}}, \hat q)\ge \mathcal{L}(X, \hat{\vec{\theta}}, q)
当且仅当分布q(\vec t)为分布\hat{q}(\vec t)时公式(2)中的等号成立。此外对任意的\vec\theta,结合公式(1)和(2)有\tag{3}\mathcal f(X, \vec\theta)\ge\mathcal{L}(X, \vec{\theta}, \hat q)当且仅当\vec\theta=\hat{\vec\theta}时公式(3)中的等号成立。
基于以上推导,EM算法的计算流程可表示如下:
- 给定\vec \theta的初始值\vec{\theta}^{(0)},按以下步骤迭代至收敛(以第k+1步为例)
- E-step:\large{\hat{q}(\vec t)=p(\vec t | X, \vec{\theta}^{(k)})=\frac{p(X, \vec{t} |\vec{\theta}^{(k)})}{p(X | \vec{\theta}^{(k)})}=\frac{ p(X | \vec{t}, \vec{\theta}^{(k)}) p(\vec t | \vec{\theta}^{(k)})}{ \int_{\vec t} p(X | \vec{t}, \vec{\theta}^{(k)}) p(\vec t | \vec{\theta}^{(k)})d_{\vec t}}}此时有\mathcal f(X,\vec{\theta}^{(k)})=\mathcal{L}(X, \vec{\theta}^{(k)}, \hat q)
- M-step:\large{\vec{\theta}^{(k+1)}=\argmax_{\vec \theta}\mathcal{L}(X, \vec{\theta}, \hat q) = \argmax_{\vec \theta}\int_{\vec t}\hat{q}(\vec t)\ln p(X, \vec t | \vec \theta ) d_{\vec t}= \argmax_{\vec \theta} E_{\hat q}\left[\ln p(X, \vec t | \vec \theta )\right]}此时若\vec{\theta}^{(k+1)} \ne \vec{\theta}^{(k)},则有\mathcal f(X,\vec{\theta}^{(k+1)})>\mathcal{L}(X, \vec{\theta}^{(k+1)}, \hat q)> \mathcal{L}(X, \vec{\theta}^{(k)}, \hat q)=\mathcal f(X,\vec{\theta}^{(k)})
变分推断
从EM算法的推导中可以看到在E-step中需要计算关于隐变量的后验分布,即
\large{\hat{q}(\vec t)=p(\vec t | X)=\frac{p(X, \vec{t} )}{p(X )}=\frac{ p(X | \vec{t}) p(\vec t)}{ \int_{\vec t} p(X | \vec{t}) p(\vec t)d_{\vec t}}}
这里为了简化符号省略了参数\vec{\theta}^{(k)},但不影响后续推导。在许多情况下\hat{q}(\vec t)的形式非常复杂,导致后续在M-step中很难给出公式E_{\hat q}\left[\ln p(X, \vec t | \vec \theta )\right]的解析形式,此时求解它的最大值需要很大的计算量。这时就可以使用变分推断对分布\hat{q}(\vec t)进行估计,变分推断的目标是在一个给定的分布集合Q中寻找到一个分布q^*,使得KL(q^*\| \hat{q})最小,即:
\large KL(q^*(\vec t)\| p(\vec t | X))=\int_{\vec t}q^*(\vec t)\ln \frac{q^*(\vec t)}{p(\vec t | X)}d_{\vec t}=\underbrace{\int_{\vec t}q^*(\vec t)\ln \frac{q^*(\vec t)}{p(X,\vec t)}d_{\vec t}}_{\large\text{在}Q中寻找\text{使该式最小的}q^*}+\ln p(X)
Mean Field近似:将\vec t分为d个部分,Q中的分布形式定义为Q=\{ q | q(\vec{t})=\prod_{i=1}^{d} q_{i}(\vec{t}_{i})\},不失一般性,为简化推导,这里令d=2,则上述公式可写为
\begin{aligned}\int_{\vec t}q^*(\vec t)\ln \frac{q^*(\vec t)}{p(X,\vec t)}d_{\vec t} &=\int_{\vec t}q_1^*(\vec t_1)q_2^*(\vec t_2)\ln \frac{q_1^*(\vec t_1)q_2^*(\vec t_2)}{p(X,\vec t)}d_{\vec t} \\ &=\int_{\vec t}q_1^*(\vec t_1)q_2^*(\vec t_2)\ln q_1^*(\vec t_1)d_{\vec t} + \int_{\vec t}q_1^*(\vec t_1)q_2^*(\vec t_2)\ln q_2^*(\vec t_2)d_{\vec t}-\int_{\vec t}q_1^*(\vec t_1)q_2^*(\vec t_2)\ln p(X,\vec t)d_{\vec t} \\ &=\int_{\vec t_1}q_1^*(\vec t_1)\ln q_1^*(\vec t_1)d_{\vec t_1}+\int_{\vec t_2}q_2^*(\vec t_2)\ln q_2^*(\vec t_2)d_{\vec t_2}-\int_{\vec t_1}\int_{\vec t_2}q_1^*(\vec t_1)q_2^*(\vec t_2)\ln p(X,\vec t)d_{\vec t_1}d_{\vec t_2}\end{aligned}
采用坐标下降法寻找最小值,首先固定q_2^*,从上式中提取出有关q_1^*的部分:
\large \int_{\vec t_1}q_1^*(\vec t_1) \left[\ln q_1^*(\vec t_1)-\underbrace{\int_{\vec t_2}q_2^*(\vec t_2)\ln p(X,\vec t)d_{\vec t_2}}_{\large h_1(\vec t_1)=E_{q_2^*}\left[\ln p(X,\vec t)\right]}\right]d_{\vec t_1}
定义分布\large z_1(\vec t_1)=\frac{e^{h_1(\vec t_1)}}{\int_{\vec t_1}e^{h_1(\vec t_1)}d_{\vec{t}_1}}=\frac{e^{h_1(\vec t_1)}}{const}则关于q_1^*的部分可写为
\large \int_{\vec t_1}q_1^*(\vec t_1)\ln \frac{q_1^*(\vec t_1)}{z_1(\vec t_1)}d_{\vec t_1}+const=KL\left(q_1^*(\vec t_1)\| z_1(\vec t_1)\right)+const
容易看出当分布\boldsymbol{q_1^*(\vec t_1)}为\boldsymbol{z_1(\vec t_1)}时上式取得最小值。接下来固定q_1^*,同理可以计算出q_2^*(\vec t_2),即:
\large q_2^*(\vec t_2)=z_2(\vec t_2)=\frac{e^{h_2(\vec t_2)}}{\int_{\vec t_2}e^{h_2(\vec t_2)}d_{\vec{t}_2}}=\frac{e^{E_{q_1^*}\left[\ln p(X,\vec t)\right]}}{const}
不断重复上述步骤直至收敛,最终可得到分布\boldsymbol{\hat{q}(\vec t)}的最优近似\boldsymbol{q_1^*(\vec t_1)q_2^*(\vec t_2)}