卡尔曼滤波（Kalman Filter）

模型定义

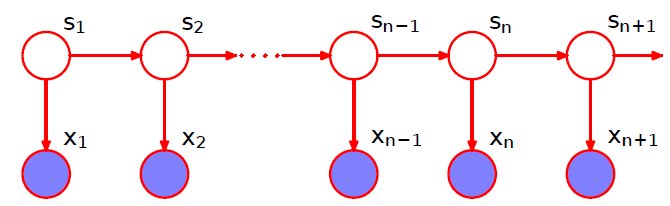
如上图所示，卡尔曼滤波（Kalman Filter）的基本模型和隐马尔可夫模型类似，不同的是隐马尔科夫模型考虑离散的状态空间，而卡尔曼滤波的状态空间以及观测空间都是连续的，并且都属于高斯分布，因此卡尔曼滤波又称为linear Gaussian Markov model，它的数学定义如下：\underbrace{s_{t}=C s_{t-1}+G h_{t}+\gamma_{t}}_{\text { latent process }}, \quad \underbrace{x_{t}=D s_{t}+\varepsilon_{t}}_{\text { observed process }}其中h_t表示控制向量(control vector)，是已知量；\gamma_{t} \sim N(0, Q)表示状态误差，它包含了状态转换公式C s_{t-1}+G h_{t}中未考虑到的其它因素，是状态转换公式准确性的度量；\varepsilon_{t} \sim N(0, V)表示观测误差，是观测精度的度量。下面举一个简单的例子：

• 假设有一个二维空间上的物体位置的观测序列（x_{t} \in \mathbb{R}^{2}），观测有一定误差；该物体的状态s_t=[p_{t1},v_{t1},p_{t2},v_{t2}]^T，其中p_t和v_t表示物体位置和速度，下标1和2表示方向；控制向量为h_t=[a_{t1},a_{t2}]^T，a_t表示加速度。由基本的物理公式可知s_{t}=\underbrace{\left[\begin{array}{cccc}{1} & {\Delta t} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {\Delta t} \\ {0} & {0} & {0} & {1}\end{array}\right]}_{C}s_{t-1}+\underbrace{\left[\begin{array}{cc} \frac{1}{2}(\Delta t)^{2} & {0} \\ {\Delta t} & {0} \\ {0} & \frac{1}{2}(\Delta t)^{2} \\ {0} & {\Delta t}\end{array}\right]}_{G}h_t+\gamma_t\text{ 以及 }x_{t}=\underbrace{\left[\begin{array}{cccc}{1} & {0} & {0} & {0} \\ {0} & {0} & {1} & {0}\end{array}\right]}_{D}s_{t}+\varepsilon_{t}

卡尔曼滤波的目标是已知观测序列x_1,x_2,\cdots,x_t，计算当前隐藏状态的分布函数，即s_{t}\left|s_{t-1} \sim N\left(C s_{t-1}+G h_{t}, Q\right), \quad x_{t}\right| s_{t} \sim N\left(D s_{t}, V\right)\quad \Rightarrow\quad p\left(s_{t} | x_{1}, \dots, x_{t}\right);\quad 1\leq t \leq T注意除观测序列以外，矩阵C,G,Q,D,V以及控制向量h_t也是给定的。

---

模型求解

• 定义S_t=(s_{t} | x_{1}, \ldots, x_{t})，容易看出S_t满足高斯分布N(\mu_{t}, \Sigma_{t})，\mu_t以及\Sigma_t即为需要求解的量
  • 为方便之后的计算，令S_{t-1}=(s_{t-1} | x_{1}, \ldots, x_{t-1})=\underbrace{\mu_{t-1}}_\text{mean}+\Delta S_{t-1},\quad \Delta S_{t-1} \sim N(0,\Sigma_{t-1})
• 定义P_t= (s_{t} | x_{1}, \ldots, x_{t-1})，有P_t=CS_{t-1}+G h_{t}+\gamma_{t}
  • 为方便之后的计算，令P_t=\underbrace{C\mu_{t-1}+Gh_t}_{\normalsize \mu_{P_t}}+\underbrace{C\Delta S_{t-1}+\gamma_t}_{\Delta P_t}，其中\Delta S_{t-1}和\gamma_t是相互独立的
• 定义O_t= (x_{t} | x_{1}, \ldots, x_{t-1})，有O_t=DP_{t}+\varepsilon_t
  • 为方便之后的计算，令O_t=\underbrace{D\mu_{P_t}}_{\normalsize \mu_{O_t}}+\underbrace{D\Delta P_t+\varepsilon_t}_{\Delta O_t}，其中\Delta P_t和\varepsilon_t是相互独立的
• 容易看出S_t=(P_t | O_t)

由上述定义可知 \left[\begin{array}{c} P_t \\ O_t \end{array}\right] \sim N\left(\left[\begin{array}{c} \mu_{P_t} \\ \mu_{O_t} \end{array}\right], \left[\begin{array}{cc} \Sigma_{PP} & \Sigma_{PO}\\ \Sigma_{PO}^T & \Sigma_{OO} \end{array}\right] \right)接下来计算协方差矩阵的这些项：

\begin{array}{c}\Sigma_{PP}=\mathbb{E}[{\Delta P_t (\Delta P_t)^T}]=C\mathbb{E}[\Delta S_{t-1} (\Delta S_{t-1})^T]C^T+\mathbb{E}[\gamma_t\gamma_t^T]=C\Sigma_{t-1}C^T+Q \\  \\ \Sigma_{PO}=\mathbb{E}[{\Delta P_t (\Delta O_t)^T}]=\mathbb{E}[\Delta P_{t} \Delta P_{t}^T]D^T+\mathbb{E}[\Delta P_{t}\varepsilon_t^T]=\Sigma_{PP}D^T \\ \\ \Sigma_{OO}=\mathbb{E}[{\Delta O_t (\Delta O_t)^T}]=D\mathbb{E}[{\Delta P_t (\Delta P_t)^T}]D^T+\mathbb{E}[\varepsilon_t\varepsilon_t^T] =D\Sigma_{PP}D^T+V \end{array}此外定义\hat{\mu}_t=\mu_{P_t}=C \mu_{t-1}+Gh_t,\space\hat{\Sigma}_t=\Sigma_{PP}=C \Sigma_{t-1} C^{T}+Q以及卡尔曼增益矩阵K_t=\Sigma_{PO}\Sigma_{OO}^{-1}=\hat{\Sigma}_{t}D^T[D\hat{\Sigma}_{t}D^T+V]^{-1}由S_t=(P_t | O_t)以及高斯分布的性质可知\tag{1}\Sigma_t=\Sigma_{PP}-\Sigma_{PO}\Sigma_{OO}^{-1}\Sigma_{PO}^T=(I-K_tD)\hat{\Sigma}_t\tag{2}\mu_t=\mu_{P_t}+\Sigma_{PO}\Sigma_{OO}^{-1}(O_t-\mu_{O_t})=\hat{\mu}_t+K_t(x_t-D\hat{\mu}_t)上述求解过程可归纳为：

1. 初始化\mu_0以及\Sigma_0
2. 预测：\hat{\mu}_t=C \mu_{t-1}+Gh_t以及\hat{\Sigma}_t=C \Sigma_{t-1} C^{T}+Q
3. 计算卡尔曼增益矩阵K_t=\hat{\Sigma}_{t}D^T[D\hat{\Sigma}_{t}D^T+V]^{-1}
4. 更新：\mu_t=\hat{\mu}_t+K_t(x_t-D\hat{\mu}_t)以及\Sigma_t=(I-K_tD)\hat{\Sigma}_t

---

Extended Kalman Filter

在Extended Kalman Filter中，状态之间的转化以及状态向观测的转化是非线性的，即s_t=g(s_{t-1},h_t)+\gamma_t,\text{  }x_{t}=f(s_{t})+\varepsilon_{t}其中g和f代表非线性函数，此时考虑使用泰勒公式将非线性函数近似为线性函数，延续上一部分的定义，有

• P_t=g(S_{t-1},h_t)+\gamma_{t}=g(\mu_{t-1}+\Delta S_{t-1},h_t)+\gamma_{t}=\underbrace{g(\mu_{t-1},h_t)}_{\normalsize \mu_{P_t}(\text{i.e., }\normalsize \hat{\mu}_t)}+\underbrace{J_g\Delta S_{t-1}+\gamma_{t}}_{\Delta P_t}
• O_t=h(P_t)+\varepsilon_t=f(\mu_{P_t}+\Delta P_t)+\varepsilon_t=f(\mu_{P_t})+J_f\Delta P_t+\varepsilon_t=\underbrace{f(\hat{\mu}_{t})}_{\normalsize \mu_{O_t}}+\underbrace{J_f\Delta P_t+\varepsilon_t}_{\Delta O_t}

其中J_g和J_f为Jacobian矩阵，假设状态为m维向量，观测为n维向量，并且g(s,h)=[g_1(s,h),\cdots,g_m(s,h)]^T以及f(s)=[f_1(s),\cdots,f_n(s)]^T，则有J_g=\left[\begin{array}{cccc}\frac{\partial g_1}{\partial \mu_{t-1,1}} & \frac{\partial g_1}{\partial \mu_{t-1,2}} & \cdots & \frac{\partial g_1}{\partial \mu_{t-1,m}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial g_m}{\partial \mu_{t-1,1}} & \frac{\partial g_m}{\partial \mu_{t-1,2}} & \cdots & \frac{\partial g_m}{\partial \mu_{t-1,m}}\end{array}\right], \text{   }J_f=\left[\begin{array}{cccc}\frac{\partial f_1}{\partial \hat{\mu}_{t,1}} & \frac{\partial f_1}{\partial \hat{\mu}_{t,2}} & \cdots & \frac{\partial f_1}{\partial \hat{\mu}_{t,m}} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial f_n}{\partial \hat{\mu}_{t,1}} & \frac{\partial f_n}{\partial \hat{\mu}_{t,2}} & \cdots & \frac{\partial f_n}{\partial \hat{\mu}_{t,m}}\end{array}\right]容易看出Extended Kalman Filter的求解过程可归纳为：

1. 初始化\mu_0以及\Sigma_0
2. 预测：\hat{\mu}_t=g(\mu_{t-1},h_t)以及\hat{\Sigma}_t=J_g \Sigma_{t-1} J_g^{T}+Q
3. 计算卡尔曼增益矩阵K_t=\hat{\Sigma}_{t}J_f^T[J_f\hat{\Sigma}_{t}J_f^T+V]^{-1}
4. 更新：\mu_t=\hat{\mu}_t+K_t[x_t-f(\hat{\mu}_t)]以及\Sigma_t=(I-K_tJ_f)\hat{\Sigma}_t

---

Unscented Kalman Filter

Unscented Kalman Filter和Extended Kalman Filter的模型定义一样，只是具体求解方法不同。相对于Extended Kalman Filter使用泰勒公式近似非线性函数，Unscented Kalman Filter通过选取多个样本点（the sigma points）直接估计均值和方差。仍然延续之前的定义，假设状态为m维向量，从随机变量S_{t-1}中选取2m+1个样本点，记为矩阵\mathcal{X}_{t-1}（m行2m+1列），选取方式为\mathcal{X}_{t-1}=\left[\begin{array}{ccc}\mu_{t-1} & \mu_{t-1}+\sqrt{(m+\lambda )}L_{t-1} & \mu_{t-1}-\sqrt{(m+\lambda )}L_{t-1} \end{array}\right]其中L_{t-1}为下三角矩阵，它是将\Sigma_{t-1}进行Cholesky分解得到的，即\Sigma_{t-1}=L_{t-1}L_{t-1}^T。接下来对每个采样点分配权重：\vec{w}=\left[\begin{array}{ccccc}\frac{\lambda}{m+\lambda} & \frac{1}{2(m+\lambda)} & \frac{1}{2(m+\lambda)} & \cdots & \frac{1}{2(m+\lambda)}\end{array}\right]\vec{w}为后续求均值和协方差矩阵时使用的权重，通常取\lambda=3-m。将\mathcal{X}_{t-1}代入函数g可以得到\hat{\mathcal{X}}_{t}=\left[\begin{array}{cccc}g(\mathcal{X}_{t-1}^{[1]},h_t) & g(\mathcal{X}_{t-1}^{[2]},h_t)  & \cdots & g(\mathcal{X}_{t-1}^{[2m+1]},h_t)\end{array}\right]其中上标表示矩阵的列数，由\hat{\mathcal{X}}_{t}可以估计出P_t的均值和方差：\tag{3}\hat{\mu}_t=\sum_{i=1}^{2m+1}w_i\hat{\mathcal{X}}_{t}^{[i]}\tag{4} \hat{\Sigma}_t=\sum_{i=1}^{2m+1}w_i(\hat{\mathcal{X}}_{t}^{[i]}-\hat{\mu}_t)(\hat{\mathcal{X}}_{t}^{[i]}-\hat{\mu}_t)^T+Q接下来可以通过两种方式得到观测的采样点\mathcal{Z}_t：

1. 直接通过\hat{\mathcal{X}}_{t}进行计算，即\mathcal{Z}_{t}=\left[\begin{array}{cccc}f(\hat{\mathcal{X}}_{t}^{[1]}) & f(\hat{\mathcal{X}}_{t}^{[2]})  & \cdots & f(\hat{\mathcal{X}}_{t}^{[2m+1]}) \end{array}\right]
2. 通过得到的\hat{\mu}_t以及\hat{\Sigma}_t重新采样，有公式\hat{\mathcal{X}}_{t}^*=\left[\begin{array}{ccc}\hat{\mu}_{t} & \hat{\mu}_{t}+\sqrt{(m+\lambda )}\hat{L}_t & \hat{\mu}_{t}-\sqrt{(m+\lambda )}\hat{L}_t \end{array}\right]其中\hat{\Sigma}_t = \hat{L}_t\hat{L}_t^T，然后计算过程同第一种方式，即\mathcal{Z}_{t}=\left[\begin{array}{cccc}f(\hat{\mathcal{X}}_{t}^{*[1]}) & f(\hat{\mathcal{X}}_{t}^{*[2]})  & \cdots & f(\hat{\mathcal{X}}_{t}^{*[2m+1]}) \end{array}\right]

同公式(3)和(4)类似，可以估计出O_t的均值和协方差矩阵：\tag{5}\mu_{O_t}=\sum_{i=1}^{2m+1}w_i\mathcal{Z}_{t}^{[i]}\tag{6}\Sigma_{OO}=\sum_{i=1}^{2m+1}w_i(\mathcal{Z}_{t}^{[i]}-\mu_{O_t})(\mathcal{Z}_{t}^{[i]}-\mu_{O_t})^T+V接下来计算矩阵\tag{7} \Sigma_{PO}=\sum_{i=1}^{2m+1}w_{i}(\hat{\mathcal{X}}_{t}^{[i]}-\hat{\mu}_{t})({\mathcal{Z}}_{t}^{[i]}-\mu_{O_t})^T注意若使用第二种方式计算\mathcal{Z}_t，需将公式(7)中的\hat{\mathcal{X}}_{t}替换为\hat{\mathcal{X}}_{t}^*。卡尔曼增益矩阵为K_t=\Sigma_{PO}\Sigma_{OO}^{-1}，由公式(1)和(2)可以计算出\tag{8} \Sigma_t=\Sigma_{PP}-\Sigma_{PO}\Sigma_{OO}^{-1}\Sigma_{PO}^T=\hat{\Sigma}_t-K_t\Sigma_{PO}^T\tag{9} \mu_t=\hat{\mu}_t+K_t[x_t-\mu_{O_t}]

Unscented Kalman Filter的求解过程可归纳为：

1. 初始化\mu_0以及\Sigma_0
2. 预测：计算\hat{\mathcal{X}}_{t}，得到\hat{\mu}_t以及\hat{\Sigma}_t
3. 计算\mathcal{Z}_{t}（从上述两种方式中选择一种），得到\mu_{O_t}、\Sigma_{OO}以及\Sigma_{PO}
4. 计算卡尔曼增益矩阵K_t=\Sigma_{PO}\Sigma_{OO}^{-1}
5. 更新：根据公式(8)和(9)计算\mu_t以及\Sigma_t