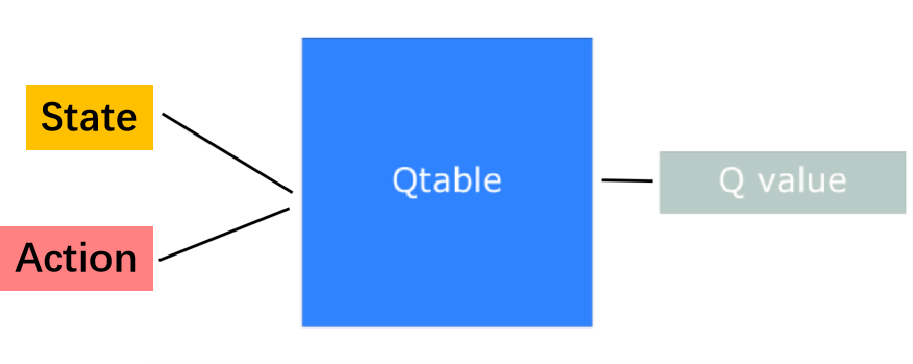
在文章强化学习：蒙特卡洛和时序差分中介绍了使用时序差分解决强化学习问题的一种经典方法：Q-Learning，但是该方法适用于有限的状态集合\mathcal{S}，一般来说使用n行(n = number of states)和m列(m= number of actions)的矩阵(Q table)来储存action-value function的值，如下图所示：
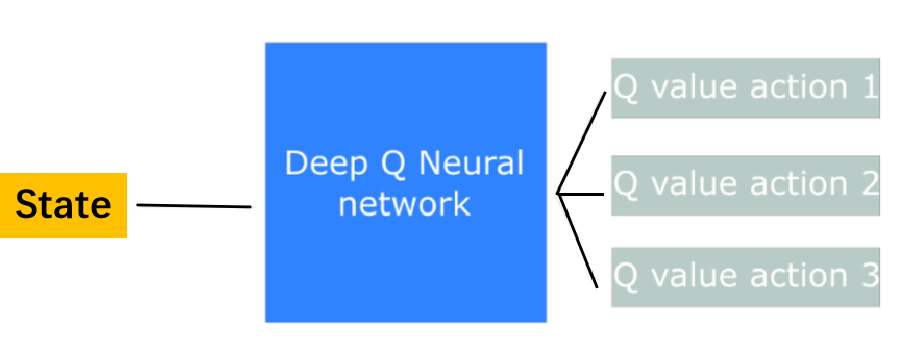
对于连续的状态集合\mathcal{S}，上述方法就不能适用了，这时可以引入神经网络来估计Q的值，即Deep Q-Learning，如下图所示：
接下来介绍Deep Q-Learning中常用的几种技巧，用于提升学习效果：
- Stack States：对于连续的状态集合，单个状态不能很好地描述整体的状况，可以使用CNN或RNN模型同时考虑多个连续的状态和它们之间的依赖关系。例如下图所示，要判断黑色方块的移动方向，仅凭一副图像是无法判断的，需要连续的多幅图像才能判断出黑色方块在向右移动。
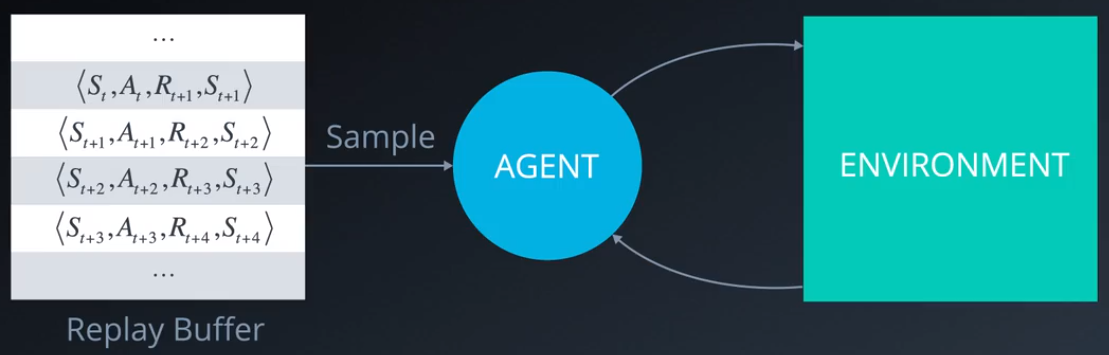
- Experience Replay：如下图所示，为了防止算法在训练过程中忘记了之前场景获得的经验，可以创建一个Replay Buffer，不断回放之前的场景对算法进行训练；另一方面，相邻的场景之间（例如[S_{t},A_{t},R_{t+1},S_{t+1}]与[S_{t+1},A_{t+1},R_{t+2},S_{t+2}]）有着一定的相关性，为了防止算法被固定在某些特定的状态空间，从Replay Buffer中随机抽样选取场景进行训练可打乱场景之间的顺序，减少相邻场景的相关性。
- Target Network：不同于Q-Learning中不断更新Q(S,A)的值使之趋向于对应最优策略\pi^*的q^*(S,A)，在Deep Q-Learning中通过对计算Q值的神经网络的权重系数\vec w不断进行更新，使神经网络成为函数q^*的近似。定义损失函数J(\vec w)=[\hat{q}(S,A,\vec w)-q_{\text{reference}}(S,A)]^2其中q_{\text{reference}}叫做TD target，为网络\hat q的近似真值，此时有\Delta \vec{w}=-\frac{\alpha}{2}\nabla_{\vec{w}}J(\vec w),\quad\vec w\gets\vec{w}+\Delta \vec{w}假设场景为[S,A,R,S^{\prime}]，q_{\text{reference}}可表示为q_{\text{reference}}(S,A)=R+\gamma \max_a\hat q(S^{\prime},a,\vec w)上述表示方式的一个缺点是TD target会随着参数\vec w的更新不断变化，加大了训练难度，减小了训练效率。一个解决方法是使用不同的神经网络（Target Network）来计算TD target，为了简化算法，Target Network通常会使用与\hat q相同的网络架构，但是每隔一定的步数才会更新其参数，对J(\vec w)计算梯度，参数更新步长可以写为
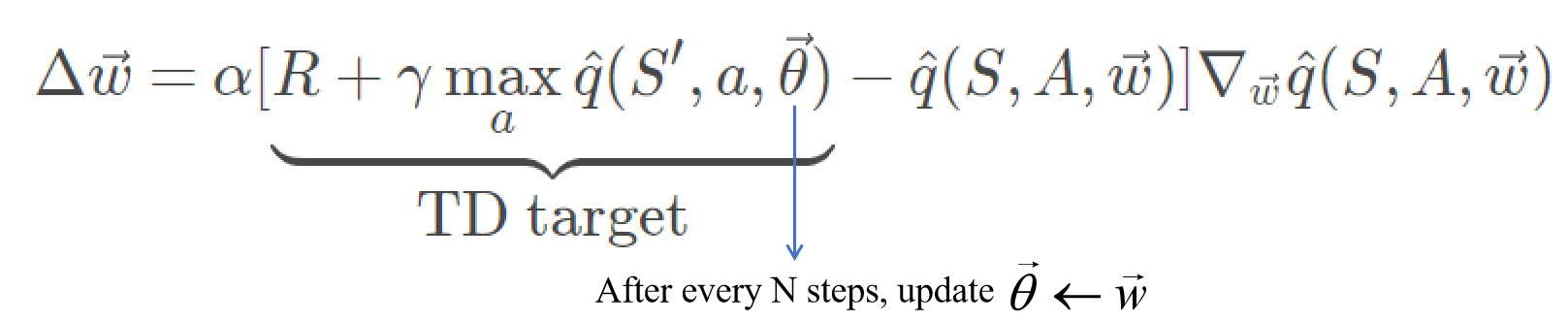
- Double DQN：为了解决TD target对\hat{q}的真值可能高估的问题（参考公式\mathbb{E}_{\pi}[\max_a Q(s,a)] \geq \max_a \mathbb{E}_{\pi}[Q(s,a)]），可以将动作a的选择过程与TD target的计算过程进行分割，此时的TD target可以写为：
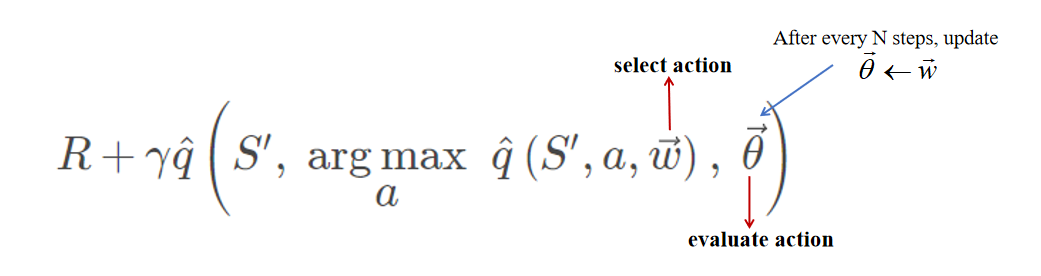
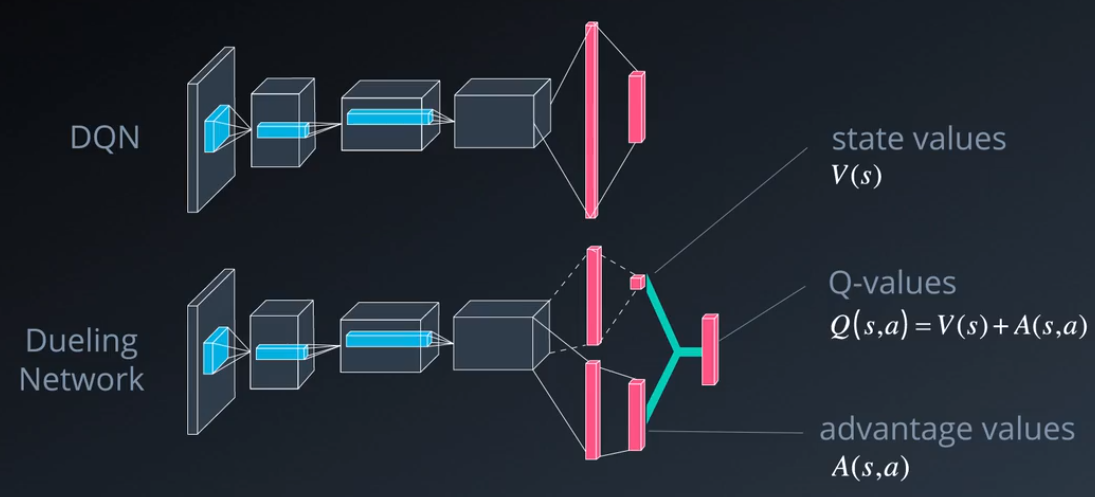
- Dueling DQN：如下图所示，相对于直接计算action-value function \hat q(s,a)，即Q(s,a)，可以将Q(s,a)分解为state-value function V(s)与advantage function A(s,a)之和，即直接对V(s)进行估计，再叠加上采取不同行动对其的影响。在实际计算中，还需对A(s,a)添加额外的限制，下面例举两种常用的方式：\begin{cases}\text{Option 1: }\max_a A(s,a)=0 \\ \text{Option 2: }\sum_a A(s,a)=0\end{cases}
代码实现
使用GYM强化学习环境，以其中的一个任务BreakoutDeterministic-v0为基础进行训练：
一、搭建强化学习环境
点击查看代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
import gym import cv2 import numpy as np import pandas as pd from gym.core import Wrapper from gym.spaces.box import Box import matplotlib.pyplot as plt """A gym wrapper that crops, scales, and stacks images into the desired shapes""" class PreprocessAtari(Wrapper): def __init__(self, env, height=64, width=64, color=False, crop=lambda img: img[32:194,:,:], n_frames=4, dim_order='tensorflow', reward_scale=1): super(PreprocessAtari, self).__init__(env) self.img_size = (height, width) self.crop = crop self.color = color self.dim_order = dim_order self.reward_scale = reward_scale n_channels = (3 * n_frames) if color else n_frames #stack n frames obs_shape = { 'theano': (n_channels, height, width), 'pytorch': (n_channels, height, width), 'tensorflow': (height, width, n_channels), }[dim_order] self.observation_space = Box(0.0, 1.0, obs_shape) self.framebuffer = np.zeros(obs_shape, 'float32') ###Resets the game, returns initial frames### def reset(self): self.framebuffer = np.zeros_like(self.framebuffer) self.update_buffer(self.env.reset()) return self.framebuffer ###Plays the game for 1 step, returns frame buffer### def step(self, action): new_img, r, done, info = self.env.step(action) self.update_buffer(new_img) return self.framebuffer, r * self.reward_scale, done, info def update_buffer(self, img): img = self.preproc_image(img) offset = 3 if self.color else 1 if self.dim_order == 'tensorflow': axis = -1 cropped_framebuffer = self.framebuffer[:, :, :-offset] else: axis = 0 cropped_framebuffer = self.framebuffer[:-offset, :, :] self.framebuffer = np.concatenate([img, cropped_framebuffer], axis=axis) ### image processing ### def preproc_image(self, img): img = self.crop(img) img = cv2.resize(img / 255, self.img_size, interpolation=cv2.INTER_LINEAR) if not self.color: img = img.mean(-1, keepdims=True) if self.dim_order != 'tensorflow': img = img.transpose([2, 0, 1]) # [h, w, c] to [c, h, w] return img.astype('float32') env = gym.make("BreakoutDeterministic-v0") #create raw env env = PreprocessAtari(env) observation_shape = env.observation_space.shape n_actions = env.action_space.n obs = env.reset() |
二、搭建卷积神经网络
点击查看代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import tensorflow as tf from tensorflow.keras.layers import Input, Conv2D, Dense, Flatten, Lambda, Add import tensorflow.keras.backend as K from tensorflow.keras.models import Model """A simple DQN agent""" class DQNAgent: ### Dueling Network ### def __init__(self, name, state_shape, n_actions, epsilon=0, reuse=False): layer0 = Input(shape=state_shape) layer1 = Conv2D(16, kernel_size=3, strides=2, padding="same", activation="relu")(layer0) layer2 = Conv2D(32, kernel_size=3, strides=2, padding="same", activation="relu")(layer1) layer3 = Conv2D(64, kernel_size=3, strides=2, padding="same", activation="relu")(layer2) layer4 = Flatten()(layer3) layer5_1 = Dense(256, activation="relu")(layer4) layer5_2 = Dense(256, activation="relu")(layer4) layer6_1 = Dense(1, activation=None)(layer5_1) layer6_2 = Dense(n_actions, activation=None)(layer5_2) layer7_2 = Lambda(lambda x: x - K.mean(x, axis=1, keepdims=True))(layer6_2) layer8 = Add()([layer6_1,layer7_2]) self.model = Model(layer0, layer8) self.epsilon = epsilon ###takes agent's observation, returns qvalues### def get_qvalues(self, state_t): qvalues = self.model(state_t) assert int(qvalues.shape[1]) == n_actions return qvalues ###pick actions given qvalues. Uses epsilon-greedy exploration strategy### def sample_actions(self, qvalues): epsilon = self.epsilon batch_size, n_actions = qvalues.shape random_actions = np.random.choice(n_actions, size=batch_size) best_actions = K.argmax(qvalues, axis=-1) should_explore = np.random.choice([0, 1], batch_size, p=[1-epsilon, epsilon]) return np.where(should_explore, random_actions, best_actions) agent = DQNAgent("dqn_agent", observation_shape, n_actions, epsilon=0.5) target_network = DQNAgent("target_network", observation_shape, n_actions) #Target Network ###assign target_network.weights variables to their respective agent.weights values### def load_weigths_into_target_network(agent, target_network): local_weights = np.array(agent.model.get_weights()) target_weights = np.array(target_network.model.get_weights()) assert len(local_weights) == len(target_weights), "Local and target model parameters must have the same size" target_network.model.set_weights(local_weights) return ###Plays n_games full games. If greedy, picks actions as argmax(qvalues). Returns mean reward.### def evaluate(env, agent, n_games=1, greedy=False, t_max=10000): rewards = [] for _ in range(n_games): s = env.reset() reward = 0 for _ in range(t_max): qvalues = agent.get_qvalues(s[None,:,:,:]) action = K.argmax(qvalues,axis=-1)[0] if greedy else agent.sample_actions(qvalues)[0] s, r, done, _ = env.step(action) reward += r if done: break rewards.append(reward) return np.mean(rewards) |
三、建立Replay Buffer
点击查看代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
import random class ReplayBuffer(object): def __init__(self, size): self._storage = [] self._maxsize = size self._next_idx = 0 def __len__(self): return len(self._storage) def add(self, obs_t, action, reward, obs_tp1, done): data = (obs_t, action, reward, obs_tp1, done) if self._next_idx >= len(self._storage): self._storage.append(data) else: self._storage[self._next_idx] = data self._next_idx = (self._next_idx + 1) % self._maxsize def _encode_sample(self, idxes): obses_t, actions, rewards, obses_tp1, dones = [], [], [], [], [] for i in idxes: data = self._storage[i] obs_t, action, reward, obs_tp1, done = data obses_t.append(np.array(obs_t, copy=False)) actions.append(action) rewards.append(reward) obses_tp1.append(np.array(obs_tp1, copy=False)) dones.append(done) return ( np.array(obses_t), np.array(actions), np.array(rewards), np.array(obses_tp1), np.array(dones) ) def sample(self, batch_size): idxes = [random.randint(0, len(self._storage) - 1) for _ in range(batch_size)] return self._encode_sample(idxes) ###Add n_steps scenes to replay buffer### def play_and_record(agent, env, exp_replay, n_steps=1): s = env.framebuffer rs = [] # Play the game for n_steps for i in range(n_steps): qvalues = agent.get_qvalues(s[None,:,:,:]) action = agent.sample_actions(qvalues)[0] s_next, r, done, _ = env.step(action) rs.append(r) exp_replay.add(s, action, r, s_next, done) s = env.reset() if done else s_next return np.array(rs).sum() exp_replay = ReplayBuffer(10**5) play_and_record(agent, env, exp_replay, n_steps=10000) |
四、训练和验证网络
点击查看代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
from tqdm import trange from IPython.display import clear_output from tensorflow.keras.optimizers import Adam batch_size = 128 gamma = 0.99 mean_rw_history = [] td_loss_history = [] optimizer = Adam(learning_rate=0.001) def moving_average(x, span=100, **kw): return pd.DataFrame({'x': np.asarray(x)}).x.ewm(span=span, **kw).mean().values for i in trange(75000): play_and_record(agent, env, exp_replay, 10) #play ### train obs_batch, act_batch, reward_batch, next_obs_batch, is_done_batch = exp_replay.sample(batch_size) is_not_done_batch = 1 - is_done_batch with tf.GradientTape() as tape: current_qvalues = agent.get_qvalues(obs_batch) Q_current = K.sum(current_qvalues * K.one_hot(act_batch, n_actions), axis=1) next_qvalues = agent.get_qvalues(next_obs_batch) next_actions = K.argmax(next_qvalues, axis=-1) #select action next_qvalues_target = target_network.get_qvalues(next_obs_batch) Q_targets_next = K.sum(next_qvalues_target * K.one_hot(next_actions, n_actions), axis=1) #evaluate action Q_targets = reward_batch + gamma * Q_targets_next * is_not_done_batch #TD target(Double DQN; set Q_targets_next=0 if done) td_loss = (Q_current - Q_targets) ** 2 td_loss = K.mean(td_loss) gradients = tape.gradient(td_loss, agent.model.trainable_weights) optimizer.apply_gradients(zip(gradients, agent.model.trainable_weights)) td_loss_history.append(td_loss) if i % 500 == 0: load_weigths_into_target_network(agent, target_network) #adjust target network parameters agent.epsilon = max(agent.epsilon * 0.985, 0.01) mean_rw_history.append(evaluate(PreprocessAtari(gym.make("BreakoutDeterministic-v0")), agent, n_games=3)) if i % 100 == 0: clear_output(True) print("buffer size = %i, epsilon = %.5f" % (len(exp_replay), agent.epsilon)) 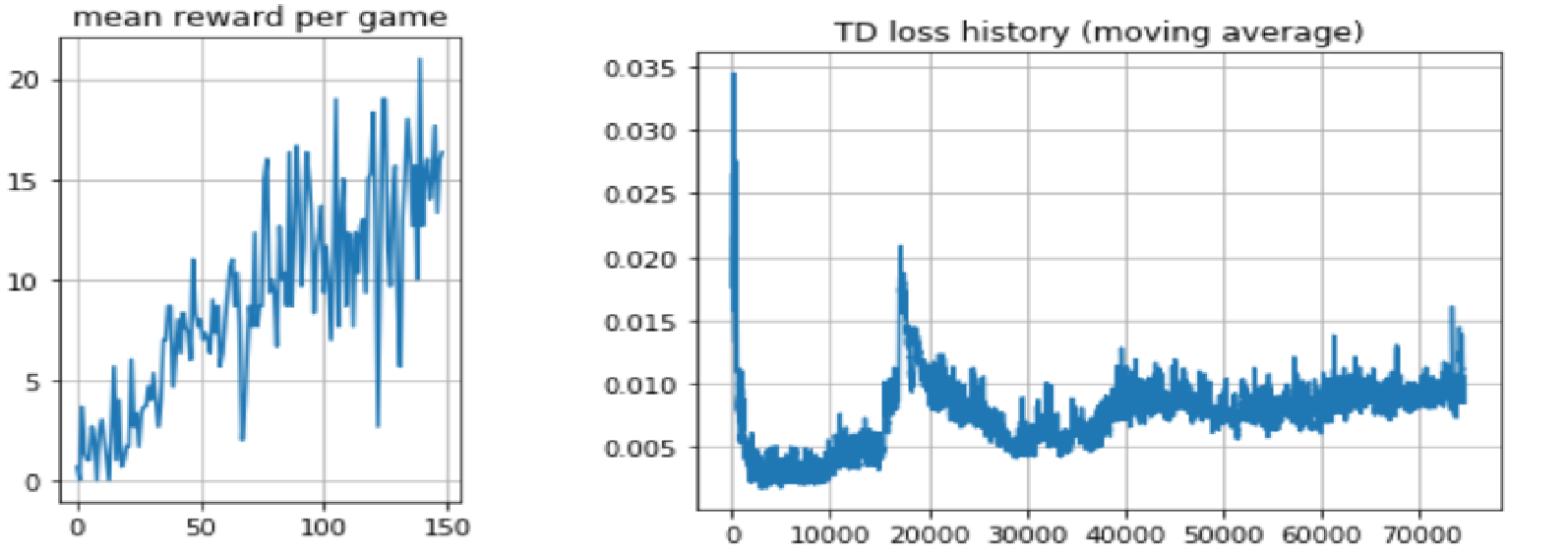plt.subplot(1, 2, 1) plt.title("mean reward per game") plt.plot(mean_rw_history) plt.grid() plt.figure(figsize=[12, 4]) plt.subplot(1, 2, 2) plt.title("TD loss history (moving average)") plt.plot(moving_average(np.array(td_loss_history), span=100, min_periods=100)) plt.grid() plt.show() |
