隐马尔科夫模型HMM介绍

马尔科夫链是描述状态转换的随机过程，该过程具备“无记忆”的性质：即当前时刻 $t$ 的状态 $s_t$ 的概率分布只由前一时刻 $t-1$ 的状态 $s_{t-1}$ 决定，与时间序列中 $t-1$ 时刻之前的状态无关。定义马尔科夫链的转移矩阵为 $\mathcal A$ ，有 $\large \mathcal{A}_{ij}=p\left(s_{t}=j | s_{t-1}=i\right),\text{ }s_{t} | s_{t-1} \sim \operatorname{Discrete}\left(\mathcal{A}_{\large s_{t-1}, :}\right)$ 容易看出矩阵 $\mathcal A$ 的每行之和为 $1$ ，给定一个起始状态 $s_1$ (也可通过某个分布产生)，可通过转移矩阵抽样生成序列 $\left(s_{1}, s_2, \dots, s_{t}\right)$ 。

模型定义

隐马尔科夫模型HMM假设观测是从一个隐藏的马尔科夫状态序列生成的，如下图所示：

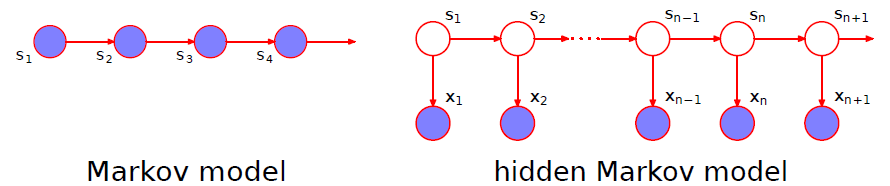
不失一般性，假设共有 $S$ 个离散状态，即 $s \in \{1,2,\dots,S\}$
不失一般性，假设共有 $X$ 种观测，即 $x \in \{1,2,\dots,X\}$
定义初始的状态分布为 $\vec{\pi}=(\pi_1,\pi_2,\dots,\pi_S)$ ，即 $s_{1} \sim \operatorname{Discrete}(\vec{\pi})$
定义状态 $s$ 的转移矩阵为 $\mathcal{A}$ ，则 $\mathcal{A}$ 为 $S$ 行 $S$ 列的矩阵，即 $s_{i} |\left\{s_{i-1}=k^{\prime}\right\} \sim \operatorname{Discrete}\left(\mathcal{A}_{k^{\prime}, :}\right)$
定义观测 $x$ 的生成概率为 $\mathcal{B}$ ，则 $\mathcal{B}$ 为 $S$ 行 $X$ 列的矩阵，即 $x_{i} |\left\{s_{i}=k^{\prime}\right\} \sim \operatorname{Discrete}\left(\mathcal{B}_{k^{\prime}, :}\right)$

则HMM的求解可归纳为以下两个问题：

训练：已知观测序列 $\vec{o}=(x_1,x_2,\dots,x_T)$ ，使用最大似然估计计算参数 $\vec{\pi},\mathcal{A},\mathcal{B}$ ，即 $\large \vec{\pi}_{\mathrm{ML}}, \mathcal{A}_{\mathrm{ML}}, \mathcal{B}_{\mathrm{ML}}=\underset{\large \vec{\pi},\mathcal{A},\mathcal{B}}{\arg \max}\space p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)$
预测：已知观测序列 $\vec{o}$ 以及参数 $\vec{\pi},\mathcal{A},\mathcal{B}$ ，估计生成观测序列 $\vec{o}$ 的最可能的隐藏状态序列 $\vec{s}=(s_{1}, \ldots, s_{T})$ ，即 $\large s_{1}, \ldots, s_{T}=\underset{\large \vec s}{\arg \max}\space\space p\left(\vec{s} | \vec{o}, \vec{\pi},\mathcal{A},\mathcal{B}\right)$

参数估计

要解决问题 $1$ ，首先看一下如何估计 $p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)$ ，根据概率公式，有 $\large{\begin{aligned} p(\vec{o} | \vec{\pi}, \mathcal{A}, \mathcal{B}) &=\sum_{s_{1}=1}^{S} \cdots \sum_{s_{T}=1}^{S} p\left(\vec{o}, s_{1}, \ldots, s_{T} | \vec{\pi}, \mathcal{A},\mathcal{B}\right) \\ &=\sum_{s_{1}=1}^{S} \cdots \sum_{s_{T}=1}^{S} \pi_{s_1}\mathcal{B}_{s_1,x_1}\prod_{i=2}^{T}\mathcal{A}_{s_{i-1},s_i}\mathcal{B}_{s_i,x_i} \end{aligned}}$ 如果按上述公式直接进行计算，复杂度为 $\mathcal{O}(TS^T)$ ，效率太低，考虑使用动态规划的思想，将算法复杂度降为 $\mathcal{O}(TS^2)$ ，可以使用两种方式：

1. Forward Algorithm

定义\alpha_{t}(j)=p\left(x_{1}, x_{2} \ldots x_{t}, s_{t}=j | \vec{\pi}, \mathcal{A},\mathcal{B}\right),\text{ }t\in\{1,2,\cdots,T\},\text{ }j\in\{1,2,\cdots,S\}，则算法可以写为：
- Initialization: $\alpha_{1}(j)=\pi_j\mathcal{B}_{j,x_1}; \quad 1 \leq j \leq S$
- Recursion: $\alpha_{t}(j)=\sum_{i=1}^{S} \alpha_{t-1}(i) \mathcal{A}_{i j} \mathcal{B}_{j,x_t} ; \quad 1 \leq j \leq S, 1\lt t \leq T$
- Termination: $p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)=\sum_{i=1}^{S} \alpha_{T}(i)$

2. Backward Algorithm

定义\beta_{t}(i)=p\left(x_{t+1}, x_{t+2} \ldots x_{T} | s_{t}=i, \vec{\pi}, \mathcal{A},\mathcal{B}\right),\text{ }t\in\{1,2,\cdots,T\},\text{ }i\in\{1,2,\cdots,S\}，则算法可以写为：
- Initialization: $\beta_{T}(i)=1; \quad 1 \leq i \leq S$
- Recursion: $\beta_{t}(i)=\sum_{j=1}^{S} \mathcal{A}_{i j} \mathcal{B}_{j,x_{t+1}} \beta_{t+1}(j) ; \quad 1 \leq i \leq S, 1 \leq t < T$
- Termination: $p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)=\sum_{j=1}^{S} \pi_{j} \mathcal{B}_{j,x_1} \beta_{1}(j)$

使用EM算法求解 $\vec{\pi}_{\mathrm{ML}}, \mathcal{A}_{\mathrm{ML}}, \mathcal{B}_{\mathrm{ML}}$ ，关于EM算法的具体介绍可参考文章EM算法和变分推断介绍。具体到该问题，又被称为Forward-Backward Algorithm(i.e., Baum-Welch Algorithm)：

假设参数的当前估计值\mathcal{\Lambda}^*=[\vec{\pi}^*,\mathcal{A}^*,\mathcal{B}^*]，则有
- E-step: 定义 $\hat{q}(\vec{s})=p(\vec{s} | \vec{o}, \mathcal{\Lambda}^*)$ ，以及 $\mathcal{L}(\vec{o},\mathcal{\Lambda},\hat q)=\mathbb{E}_{\hat q}[\ln p(\vec{o}, \vec{s} | \mathcal{\Lambda})]$ 。容易看出 $\ln p(\vec{o}, \vec{s} | \mathcal{\Lambda})= \underbrace{\ln \pi_{s_1}}_{\text{ initial state }} +\sum_{t=2}^{T} \underbrace{\ln \mathcal{A}_{s_{t-1}, s_t}}_{\text { Markov chain }} + \sum_{t=1}^{T} \underbrace{\ln \mathcal{B}_{s_t, x_t}}_{\text { observations }}$ 因此 $\mathcal{L}$ 的形式可写为 $\mathcal{L}(\vec{o},\mathcal{\Lambda},\hat q)=\sum_{k=1}^{S} \gamma_{1}(k) \ln \pi_{k}+\sum_{t=2}^{T} \sum_{j=1}^{S} \sum_{k=1}^{S} \xi_{t}(j, k) \ln \mathcal{A}_{j, k}+\sum_{t=1}^{T} \sum_{k=1}^{S} \gamma_{t}(k) \ln \mathcal{B}_{k, x_{t}}$ 其中 $\gamma_t(k)=p(s_t=k | \vec{o}, \mathcal{\Lambda}^*),\text{ }\xi_t(j,k)=p(s_{t-1}=j,s_t=k | \vec{o}, \mathcal{\Lambda}^*)$ ，由贝叶斯公式可知 $\large{\begin{cases} \gamma_t(k)=\frac{\large p(\vec{o}, s_t=k | \mathcal{\Lambda}^*)}{\large p(\vec{o} | \mathcal{\Lambda}^*)}=\frac{\large \alpha_t(k)\beta_t(k)}{\large \sum_{m=1}^S\alpha_t(m)\beta_t(m)} \\ \xi_t(j,k)=\frac{\large p(\vec{o}, s_{t-1}=j, s_t=k | \mathcal{\Lambda}^*)}{\large p(\vec{o} | \mathcal{\Lambda}^*)}=\frac{\large \alpha_{t-1}(j)\mathcal{A}_{jk}^*\mathcal{B}_{k,x_t}^*\beta_t(k)}{\large \sum_{m=1}^S\alpha_t(m)\beta_t(m)} \end{cases}}$ 注意此时的 $\alpha_t(\cdot)$ 以及 $\beta_t(\cdot)$ 是从参数的当前估计值 $\mathcal{\Lambda}^*$ 计算出来的
- M-step: 更新参数的估计值 $\mathcal{\Lambda}^*=\underset{\mathcal{\Lambda}}{\arg\max}\space\mathcal{L}(\vec{o},\mathcal{\Lambda},\hat q)$ ，有 $\pi_{k}^*=\frac{\gamma_{1}(k)}{\sum_{j=1}^S \gamma_{1}(j)}, \quad \mathcal{A}_{jk}^*=\frac{\sum_{t=2}^{T} \xi_{t}(j, k)}{\sum_{t=2}^{T} \sum_{l=1}^{S} \xi_{t}(j, l)}, \quad \mathcal{B}_{kv}^*=\frac{\sum_{t=1}^{T} \gamma_{t}(k) I\left(x_{t}=v\right)}{\sum_{t=1}^{T} \gamma_{t}(k)}$ 在实际应用中使用的不仅仅是 $1$ 个观测序列，假设有 $N$ 个序列，每个序列的长度为 $T_n,\text{ }n\in\{1,2,\cdots,N\}$ ，则每个序列可以计算出自己的 $\gamma_t$ 和 $\xi_t$ ，记为 $\gamma_t^{(n)}$ 和 $\xi_t^{(n)}$ ，更新公式变为 $\pi_{k}^*=\frac{\sum_{n=1}^{N} \gamma_{1}^{(n)}(k)}{\sum_{n=1}^{N} \sum_{j=1}^S \gamma_{1}^{(n)}(j)}, \quad \mathcal{A}_{jk}^*=\frac{\sum_{n=1}^{N} \sum_{t=2}^{T_{n}} \xi_{t}^{(n)}(j, k)}{\sum_{n=1}^{N} \sum_{t=2}^{T_{n}} \sum_{l=1}^{S} \xi_{t}^{(n)}(j, l)}, \quad \mathcal{B}_{kv}^*=\frac{\sum_{n=1}^{N} \sum_{t=1}^{T_{n}} \gamma_{t}^{(n)}(k) I\left(x_{t}^{(n)}=v\right)}{\sum_{n=1}^{N} \sum_{t=1}^{T_{n}} \gamma_{t}^{(n)}(k)}$

迭代上述步骤直到收敛为止

隐藏状态序列估计

为了解决问题 $2$ ，仍使用动态规划的思想(Viterbi Algorithm)，定义 $v_{t}(j)=\underset{s_{1}, \ldots, s_{t-1}}{\max} p\left(s_{1}, \ldots s_{t-1}, x_{1}, x_{2}, \ldots x_{t}, s_{t}=j | \mathcal{\Lambda}\right)$ ，此外还要定义 $b_t(j)$ 用来存储 $v_{t}(j)$ 对应的 $s_{t-1}$ ，则算法可以写为

Initialization: $v_1(j)=\pi_j\mathcal{B}_{j,x_1},\text{ }b_1(j)=0; \quad 1 \leq j \leq S$
Recursion: $\begin{array}{ll}v_{t}(j)=\underset{i \in\{1,2, \cdots, S\}}{\max} v_{t-1}(i) \mathcal{A}_{i j} \mathcal{B}_{j, x_{t}} ; \quad 1 \leq j \leq S, 1<t \leq T \\ b_{t}(j)=\underset{i \in\{1,2, \cdots, S\}}{\arg \max } v_{t-1}(i) \mathcal{A}_{i j} \mathcal{B}_{j, x_{t}} ; \quad 1 \leq j \leq S, 1<t \leq T \end{array}$
Termination: $\begin{aligned} & \text { The best score: } P^*=\max _{\vec{s}} p\left(\vec{s},\vec{o} | \mathcal{\Lambda} \right)=\max _{i\in\{1,2,\cdots,S\}} v_{T}(i) \\ & \text { The start of backtrace: } s_{T}^*=\underset{i\in\{1,2,\cdots,S\}}{\operatorname{argmax}} v_{T}(i) \end{aligned}$
Backtrace: $s_{t}^*=b_{t+1}(s_{t+1}^*); \quad 1 \leq t<T$ 容易看出 $s_1^*,s_2^*,\ldots,s_T^* = \underset{\vec s}{\arg\max}\space\space p\left(\vec{s},\vec{o}| \mathcal{\Lambda}\right)=\underset{\vec s}{\arg\max}\space\space p\left(\vec{s}|\vec{o},\mathcal{\Lambda}\right)$

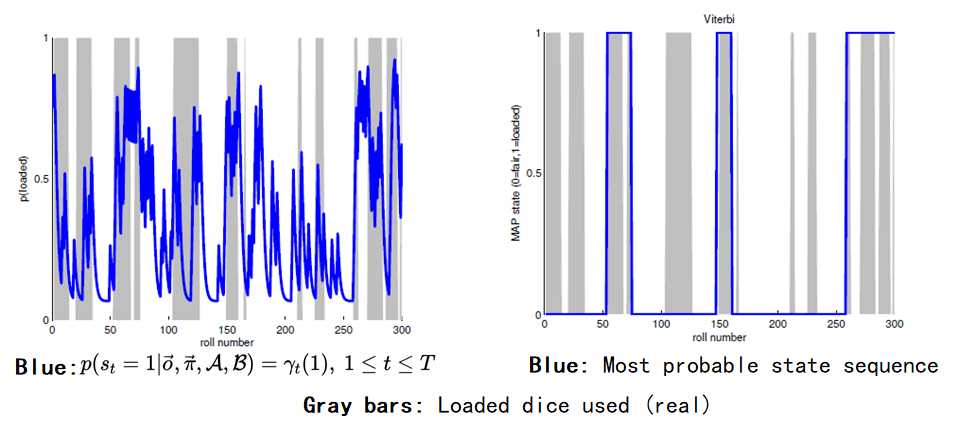
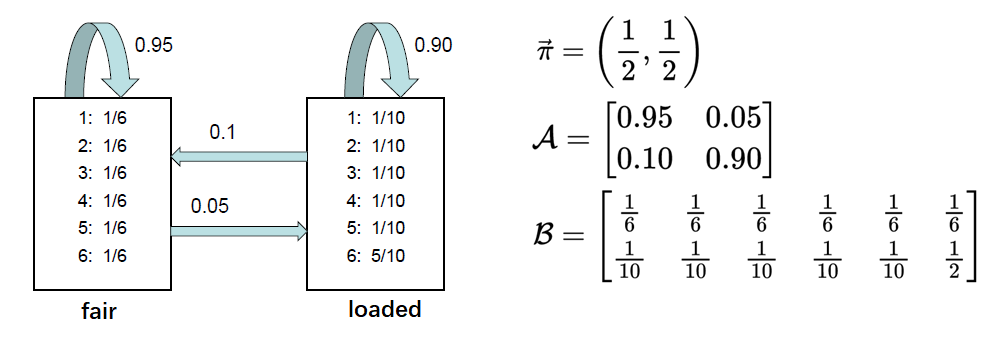
下面介绍一个使用HMM的简单例子：假设有两个骰子，一个未经处理（fair, 记为 $0$ ），一个经过处理（loaded, 记为 $1$ ）。每次投掷时使用前一次投掷的骰子，或者使用另一个骰子，观测序列是多次投掷所得到的骰子点数序列。假设真实的参数如下图所示，目标是通过观测序列估计真实的参数，进而估计出每次投掷使用的是哪个骰子。

最终的结果如下图所示，右图表示使用Viterbi算法得到的最可能的隐藏状态序列（即每次投掷使用了哪种骰子），注意左图进行简单地四舍五入后的结果不等于右图，因为左图并没有考虑状态之间的关联。

模型定义

参数估计

隐藏状态序列估计

Leave a Comment Cancel Reply