机器学习中的数据准备

数据准备是机器学习中一项非常重要的环节，本文主要对数据准备流程进行简单的梳理，主要参考了Data Preparation for Machine Learning一书。

数据准备需要进行的工作主要分为以下几类：

• 数据清理（Data Cleaning）
• 数据转换（Data Transformation）
• 特征选择（Feature Selection）

数据清理

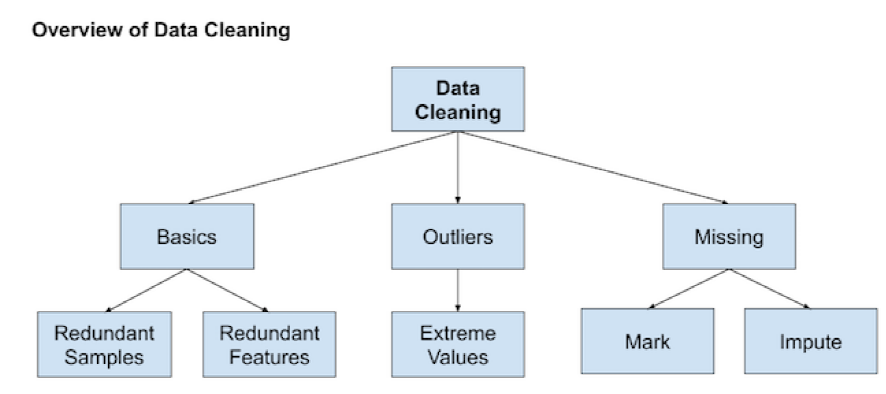
• 删除冗余的特征或样本
  # delete columns with a single unique value counts = df.nunique() to_del = [c for c,v in zip(df.columns, counts) if v==1] df.drop(to_del, axis=1, inplace=True) # delete rows of duplicate data from the dataset df.drop_duplicates(inplace=True)

  1 2 3 4 5 6

  # delete columns with a single unique value counts = df.nunique() to_del = [c for c,v in zip(df.columns, counts) if v==1] df.drop(to_del, axis=1, inplace=True) # delete rows of duplicate data from the dataset df.drop_duplicates(inplace=True)

• 寻找异常点
  • 统计学方法
    • 若特征属于正态分布N(\mu,\sigma^2)，则区间[\mu-3\sigma,\text{  }\mu+3\sigma]之外的值可视为异常值
    • 若特征属于偏态分布，则定义IQR = 75\text{th quantile} - 25\text{th quantile}，区间[25\text{th quantile} - c*IQR,  75\text{th quantile} + c*IQR]之外的值可视为异常值，c通常取1.5或3
  • 自动检测方法
    • Local Outlier Factor (LOF)：LOF算法原理介绍
      # identify outliers in the training dataset lof = LocalOutlierFactor() yhat = lof.fit_predict(X_train) # Method 1: select all rows that are not outliers mask = (yhat != -1) X_train, y_train = X_train[mask, :], y_train[mask] # Method 2: check LOF score score = lof.negative_outlier_factor_ X_train, y_train = X_train[score>threshold], y_train[score>threshold]

      1 2 3 4 5 6 7 8 9

      # identify outliers in the training dataset lof = LocalOutlierFactor() yhat = lof.fit_predict(X_train) # Method 1: select all rows that are not outliers mask = (yhat != -1) X_train, y_train = X_train[mask, :], y_train[mask] # Method 2: check LOF score score = lof.negative_outlier_factor_ X_train, y_train = X_train[score>threshold], y_train[score>threshold]

    • Isolation Forest: Isolation Forest算法原理介绍
      rng = np.random.RandomState(42) clf = IsolationForest(max_samples=256, random_state=rng, contamination='auto') yhat = clf.fit_predict(X_train) mask = (yhat != -1) X_train, y_train = X_train[mask, :], y_train[mask]

      1 2 3 4 5

      rng = np.random.RandomState(42) clf = IsolationForest(max_samples=256,  random_state=rng, contamination='auto') yhat = clf.fit_predict(X_train) mask = (yhat != -1) X_train, y_train = X_train[mask, :], y_train[mask]

• 处理缺失值
  • 直接删除有缺失值的数据
  • 使用特征的统计量(数值特征：平均值或中位数；类别特征：众数)进行填充
    # define imputer imputer = SimpleImputer(strategy=...) # fit on the training dataset (fit函数仅在训练数据上使用，防止data leakage) Xtrans = imputer.fit_transform(X_train)

    1 2 3 4

    # define imputer imputer = SimpleImputer(strategy=...) # fit on the training dataset (fit函数仅在训练数据上使用，防止data leakage) Xtrans = imputer.fit_transform(X_train)

  • 将缺失值单独标记为一个新的类别，例如'Missing'，适用于类别特征
  • 加入一个新的特征(二值变量，取值为0或1)，来对应某个特征是否缺失(1: 缺失，0: 正常)。该方法通常和其它缺失值填充方法配合使用
  • k-Nearest Neighbour Imputation
    pipeline = Pipeline(steps=[('i', KNNImputer(n_neighbors=...)), ('m', RandomForestClassifier())]) # evaluate the model cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

    1 2 3 4

    pipeline = Pipeline(steps=[('i', KNNImputer(n_neighbors=...)), ('m', RandomForestClassifier())]) # evaluate the model cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

  • Iterative Imputation
    ''' 1. 对每个缺失值进行初始填充 2. 根据选定的特征顺序依次对特征建立预测模型，将其表示为其它特征的函数， 使用该特征未缺失的数据训练模型并预测该特征的缺失值，使用预测值更新缺失值 3. 不断重复上一步骤进行迭代 ''' # estimator: 使用的预测模型 # imputation_order: 进行缺失值更新和填充的特征顺序 # n_nearest_features: 模型训练和预测使用的特征数量 # max_iter: 最大迭代次数 # initial_strategy: 初始填充使用的填充策略 pipeline = Pipeline(steps=[('i', IterativeImputer(estimator=..., max_iter=..., n_nearest_features=..., initial_strategy=..., imputation_order=...)), ('m', RandomForestClassifier())]) # evaluate the model cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

    ''' 1. 对每个缺失值进行初始填充 2. 根据选定的特征顺序依次对特征建立预测模型，将其表示为其它特征的函数，    使用该特征未缺失的数据训练模型并预测该特征的缺失值，使用预测值更新缺失值 3. 不断重复上一步骤进行迭代 '''   # estimator: 使用的预测模型 # imputation_order: 进行缺失值更新和填充的特征顺序 # n_nearest_features: 模型训练和预测使用的特征数量 # max_iter: 最大迭代次数 # initial_strategy: 初始填充使用的填充策略 pipeline = Pipeline(steps=[('i', IterativeImputer(estimator=..., max_iter=..., n_nearest_features=..., initial_strategy=..., imputation_order=...)), ('m', RandomForestClassifier())]) # evaluate the model cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=cv, n_jobs=-1)

数据转换

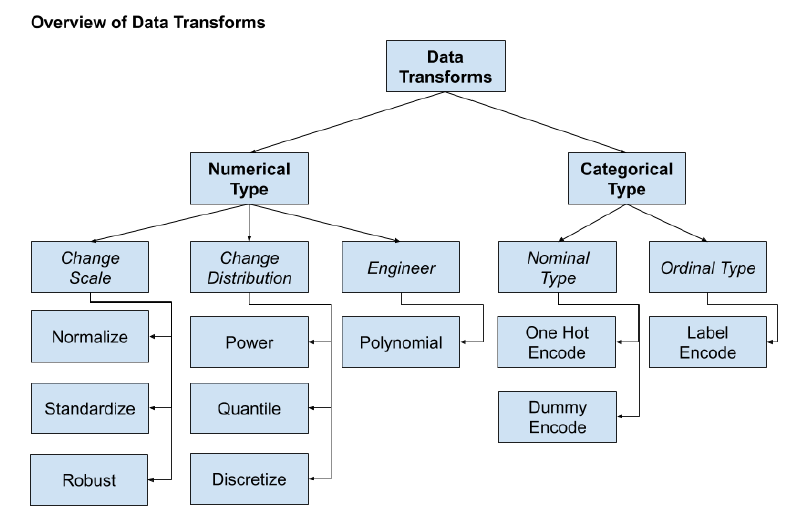
• 数值特征的尺度变换
  • Data Normalization: 将特征变换到[0,1]之间。\frac{value - min}{max - min}, MinMaxScaler()
  • Data Standardization: 将特征均值变为0，标准差变为1。\frac{value - mean}{\sigma}, StandardScaler()
  • Robust Scale: 类似Data Standardization，但选用较稳健的特征统计量(median、IQR)，减少异常值对特征统计量的影响。\frac{value - median}{IQR}, RobustScaler()
• 数值特征的分布变换
  • 将特征转换为高斯分布可以增加一些模型的预测准确度
    • Power Transform ( e.g., \ln{x},\text{ }\sqrt{x} ): PowerTransformer(method=...)，对原始特征进行尺度变换之后使用该方法有时会比直接使用产生更好效果
    • Quantile Transform: 利用累积分布函数(CDF)将特征的分布直接映射成高斯分布，QuantileTransformer(output_distribution='normal')
  • 特征离散化，即转换为类别特征，主要有下图所示的三种方法
    KBinsDiscretizer(n_bins=..., encode=..., strategy=...)
    
• 类别特征的编码
  • One-Hot Encode: 如果一个类别特征中共有k个类别，则将该特征转换为k个新的二值特征(例如"颜色：红、黄、绿"变为："颜色_红：1、0、0"以及"颜色_黄：0、1、0"以及"颜色_绿：0、0、1")，常用于决策树模型，例如CART、RandomForest，函数API为OneHotEncoder(drop=None, ...)；或者将其转换为k-1个新的特征(例如"颜色：红、黄、绿"变为："颜色_黄：0、1、0"以及"颜色_绿：0、0、1")，常用于包含偏差项(i.e., bias term)的模型，例如线性回归，函数API为OneHotEncoder(drop=‘first’, ...)
  • One-Hot Encode for Top Categories：如果一个类别特征中包含的类别较多，可将特征中出现频率较低的一些类别合成为一个类别，然后使用one-hot encode
  • Ordinal Encode: 将特征中的类别按顺序编码为0,1,2,\cdots，OrdinalEncoder()
  • Frequency Encode：将特征中的类别编码为该类别在特征中出现的频率
  • Mean Encode: 将特征中的类别编码为该类别对应的目标变量y的均值
  • Ordered Integer Encode: 按照特征中每个类别对应的目标变量y的均值从大到小将类别编码为0,1,2,\cdots
• 特征工程
  • 生成Polynomial Features: PolynomialFeatures(degree=..., interaction_only=..., include_bias=...)
  • Deep Feature Synthesis (深度特征综合): 可同时处理多个数据表进行转换 (transformation) 或聚合 (aggregation) 操作，自动生成新的特征。使用方式可参考自动化特征工程—Featuretools
• 上述技术有一些也可用于目标变量y上，例如在y上进行Power Transform可以减少它的偏度(skewness)，使之更接近高斯分布。可使用TransformedTargetRegressor对y进行转换，例如：
  # prepare the model with input scaling and power transform steps = list() steps.append(('scale', MinMaxScaler(feature_range=(1e-5,1)))) steps.append(('power', PowerTransformer())) steps.append(('model', HuberRegressor())) pipeline = Pipeline(steps=steps) # prepare the model with target power transform model = TransformedTargetRegressor(regressor=pipeline, transformer=PowerTransformer()) # evaluate model cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)

  1 2 3 4 5 6 7 8 9 10 11

  # prepare the model with input scaling and power transform steps = list() steps.append(('scale', MinMaxScaler(feature_range=(1e-5,1)))) steps.append(('power', PowerTransformer())) steps.append(('model', HuberRegressor())) pipeline = Pipeline(steps=steps) # prepare the model with target power transform model = TransformedTargetRegressor(regressor=pipeline, transformer=PowerTransformer()) # evaluate model cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1) scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)

• 可使用ColumnTransformer对不同的特征进行不同的转换，例如：
  # determine categorical and numerical features numerical_ix = X.select_dtypes(include=['int64', 'float64']).columns categorical_ix = X.select_dtypes(include=['object', 'bool']).columns # define the data preparation for the columns t = [('cat', OneHotEncoder(), categorical_ix), ('num', MinMaxScaler(), numerical_ix)] col_transform = ColumnTransformer(transformers=t, remainder=...) # define the data preparation and modeling pipeline pipeline = Pipeline(steps=[('prep',col_transform), ('m', model)])

  1 2 3 4 5 6 7 8

  # determine categorical and numerical features numerical_ix = X.select_dtypes(include=['int64', 'float64']).columns categorical_ix = X.select_dtypes(include=['object', 'bool']).columns # define the data preparation for the columns t = [('cat', OneHotEncoder(), categorical_ix), ('num', MinMaxScaler(), numerical_ix)] col_transform = ColumnTransformer(transformers=t, remainder=...) # define the data preparation and modeling pipeline pipeline = Pipeline(steps=[('prep',col_transform), ('m', model)])

特征选择

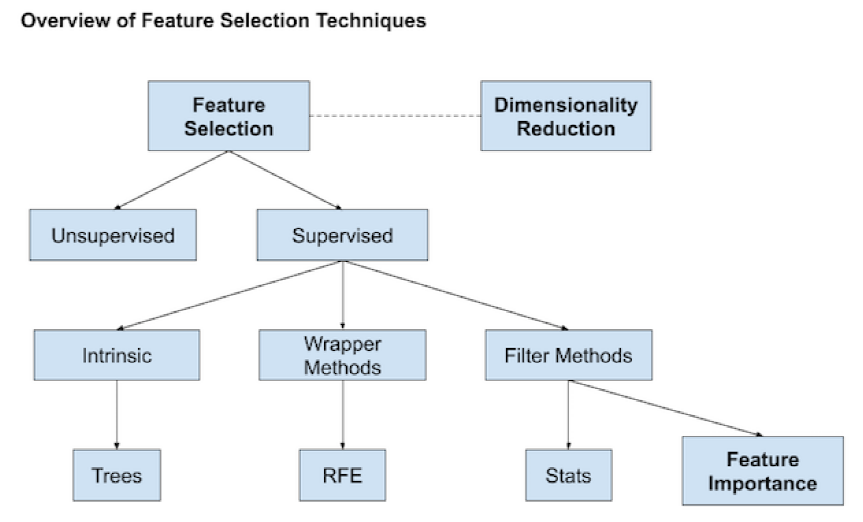
• Filter Methods
  • 统计方法
    • {\chi}^2 Test: 适用于分类问题，只能用于非负特征的选择，具体介绍可参考这篇文章
      SelectKBest(score_func=chi2, k=...)

      1	SelectKBest(score_func=chi2, k=...)

    • Mutual Information: I(X ; Y)=\int_{Y} \int_{X} p(x, y) \log \left(\frac{p(x, y)}{p(x) p(y)}\right) d x d y,\text{  }I(X ; Y)\ge 0\text{且仅在}X\text{和}Y\text{相互独立时}为0
      SelectKBest(score_func=mutual_info_classif, k=...) #分类问题 SelectKBest(score_func=mutual_info_regression, k=...) #回归问题

      1 2	SelectKBest(score_func=mutual_info_classif, k=...)  #分类问题 SelectKBest(score_func=mutual_info_regression, k=...)  #回归问题

    • One-Way ANOVA: 适用于分类问题，用于数值特征的选择
      SelectKBest(score_func=f_classif, k=...)

      1	SelectKBest(score_func=f_classif, k=...)

    • Pearson Correlation:  适用于回归问题，用于数值特征的选择
      SelectKBest(score_func=f_regression, k=...)

      1	SelectKBest(score_func=f_regression, k=...)

  • 特征重要性
    • feature importance from model coefficients (model.coef_)
      SelectFromModel(estimator=..., max_features=..., threshold=...)

      1	SelectFromModel(estimator=..., max_features=..., threshold=...)

    • feature importance from decision trees (model.feature_importances_)
      SelectFromModel(estimator=..., max_features=..., threshold=...)

      1	SelectFromModel(estimator=..., max_features=..., threshold=...)

    • feature importance from permutation testing: 将一个选定的模型训练好之后，将训练集或验证集上的某个特征的值随机打乱顺序，打乱顺序前后模型在该数据集上预测能力的变化反映了该特征的重要程度
      ### Example 1 ### model = KNeighborsRegressor() model.fit(X_train, y_train) # fit the model # perform permutation importance results = permutation_importance(model, X_train, y_train, scoring='neg_mean_squared_error') importance = results.importances_mean #get importance ### Example 2 ### model = Ridge(alpha=1e-2).fit(X_train, y_train) r = permutation_importance(model, X_val, y_val, n_repeats=30, random_state=0) importance = r.importances_mean

      1 2 3 4 5 6 7 8 9 10 11

      ### Example 1 ### model = KNeighborsRegressor() model.fit(X_train, y_train) # fit the model # perform permutation importance results = permutation_importance(model, X_train, y_train, scoring='neg_mean_squared_error') importance = results.importances_mean  #get importance   ### Example 2 ### model = Ridge(alpha=1e-2).fit(X_train, y_train) r = permutation_importance(model, X_val, y_val, n_repeats=30, random_state=0) importance = r.importances_mean

• Recursive Feature Elimination (RFE): 对选定的模型进行迭代训练，每次训练后根据得到的特征重要性删除一些特征，在此基础上重新进行训练
  RFE(estimator=..., n_features_to_select=..., step=...)

  1	RFE(estimator=..., n_features_to_select=..., step=...)

•  Dimension Reduction: LDA(有监督降维), PCA(无监督降维)，算法原理可参考PCA与LDA降维