问题描述
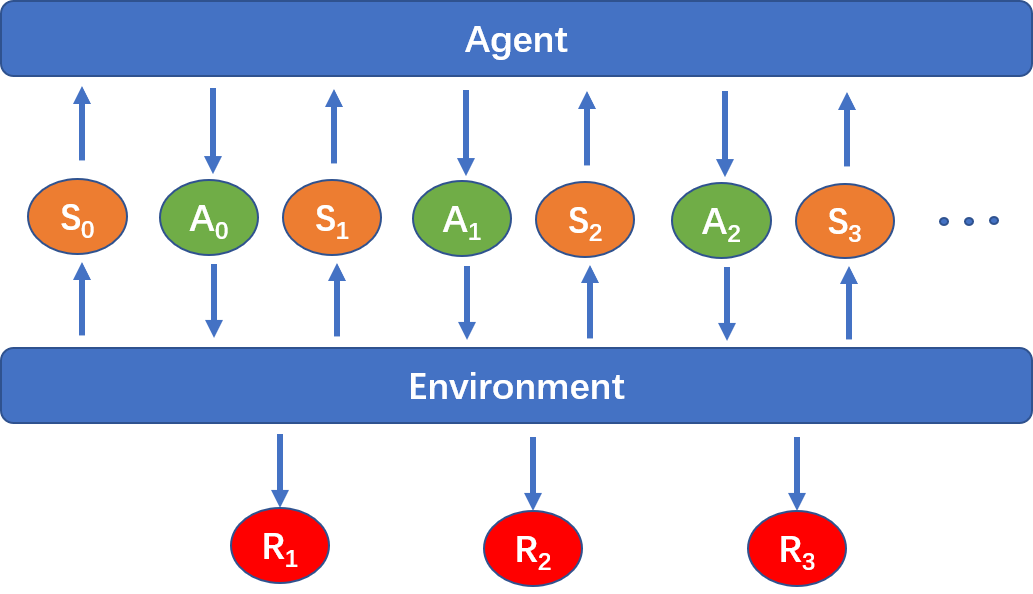
如下图所示,一个强化学习问题主要由智能体 (Agent) 和环境 (Environment) 构成,假设在时刻t环境有一个状态S_t,智能体根据状态S_t计算出对应的动作A_t,并将动作A_t传入环境中进行交互,获得对应的奖励R_{t+1},此时环境中的状态更新为S_{t+1},接着不断重复上述过程。
强化学习问题可以分为两类:
- Episodic Task:有明确的结束信号,即有一个终止状态 (Terminal State),记为S_f。当环境状态为S_f时就会结束与智能体的交互
- Continuing Task:没有明确的结束信号,环境与智能体的交互可以不断进行下去
强化学习问题中环境状态的更新可以看成一个马尔可夫决策过程 (MDP),它是一个随机过程,转换概率记为p\left(s^{\prime}, r \mid s, a\right),即给定当前时刻的状态和动作为s和a,更新后的下一时刻的状态为s^{\prime}且奖励为r的概率。需要注意的是这个转换概率与时刻t无关,即对任意时刻t,均有p\left(s^{\prime}, r \mid s, a\right) =\mathbb{P}\left(S_{t+1}=s^{\prime}, R_{t+1}=r \mid S_{t}=s, A_{t}=a\right)
时刻t的未来累积奖励记为G_t:G_t=\sum_{k=t+1}^T \gamma^{k-t-1}R_{k},\space\space 0\le\gamma\le 1若强化学习问题为Episodic Task,T即为环境状态变为终止状态S_f的时刻;若强化学习问题为Continuing Task,T\rightarrow\infty,并且\gamma需严格小于1。
智能体的目标是构建出一个策略 (Policy) \pi,策略形式可以分为两种:
- 确定性策略:\pi (s) = a,即给定状态s,得到确定的动作a
- 随机性策略:\pi (a|s) = p(A_t=a|S_t=s),即给定状态s,得到采取动作a的概率。确定性策略可以看成随机性策略的一种特殊形式。
给定策略\pi,可以定义两个关键函数:
- State-Value Function:v_{\pi}(s)=\mathbb{E}_{\pi}[G_t|S_t=s],即给定状态s,在采用策略\pi的情况下所能获得的未来累积奖励的期望值
- Action-Value Function:q_{\pi}(s,a)=\mathbb{E}_{\pi}[G_t|S_t=s,A_t=a],即给定状态s以及智能体接下来采取的动作a,在采用策略\pi的情况下所能获得的未来累积奖励的期望值
由MDP的性质容易看出这两个函数同样与时刻t无关,q_{\pi}(s,a)和v_{\pi}(s)有如下联系:\tag{1} \begin{cases} v_{\pi}(s)=\sum_a\pi(a\mid s)q_{\pi}(s,a) \\ q_{\pi}(s,a)=\sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left(r+\gamma \mathbb{E}_{\pi}\left[G_{t+1} \mid S_{t+1}=s^{\prime}\right]\right)=\sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)[r+\gamma v_{\pi}(s^{\prime})]\end{cases}由公式(1)可以看出v_{\pi}(s)有如下性质:\tag{2} v_{\pi}(s) =\sum_{a} \pi(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}(s^{\prime})\right]上述公式(2)也叫做关于State-Value Function的Bellman方程。同理可以由公式(1)推出关于Action-Value Function的Bellman方程:\tag{3} q_{\pi}(s,a) = \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \sum_{a^{\prime}}\pi(a^{\prime} \mid s^{\prime})q_{\pi}(s^{\prime},a^{\prime})\right]
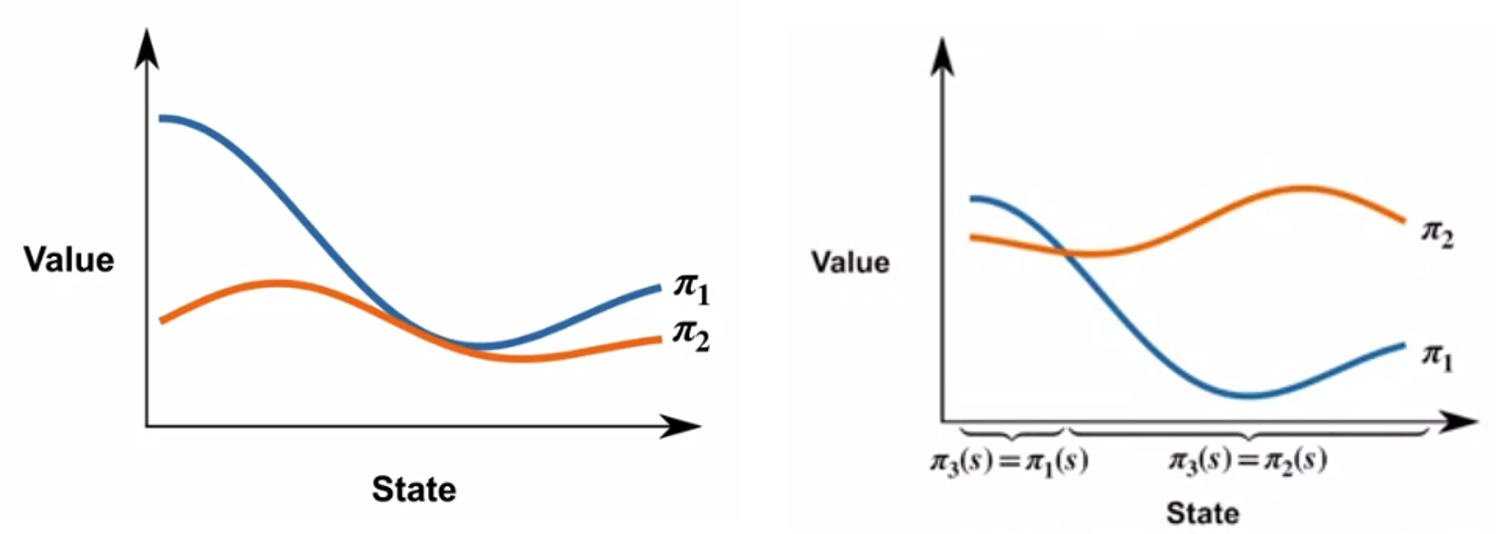
接下来定义如何比较两个策略的好坏,如下方左图所示,此时可以认为策略\pi_1优于策略\pi_2,即\pi_1 \geq \pi_2 \Longleftrightarrow v_{\pi_1}(s) \geq v_{\pi_2}(s) \text { for all possible } s根据公式(1)容易看出若令策略\pi^{\prime}(s)=\argmax_{a}q_{\pi}(s,a),则\pi^{\prime}\ge\pi,即\tag{4} v_{\pi^{\prime}}(s)=\max_a q_{\pi}(s,a)\ge\sum_a\pi(a\mid s)q_{\pi}(s,a)=v_{\pi}(s)\text{ for all possible }s智能体能获得的最优策略 (Optimal Policy) \pi^*满足\pi^*\geq \pi \text{ for all possible }\pi可以证明最优策略总是存在的(不一定唯一),例如下方右图所示的两个不能直接比较的策略\pi_1和\pi_2,可以按照图中所示的方法构建策略\pi_3,使得\pi_3优于\pi_1和\pi_2
容易看出最优策略\pi^*的state-value function v^*(s)以及action-value function q^*(s,a)有以下性质:\tag{5} \begin{cases}v^*(s)=\underset{\pi}{\max}\space\space v_{\pi}(s) \space\space\text{ for all possible }s \\ q^*(s,a)=\underset{\pi}{\max}\space\space q_{\pi}(s,a) \space\space\text{ for all possible }s\text{ and }a\end{cases}根据上述性质(5),将v^*(s)代入Bellman方程(2)中有如下等式:\tag{6} \begin{aligned}v^*(s) & =\sum_{a} \pi^*(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v^*(s^{\prime})\right] \\ & =\max_a\sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v^*(s^{\prime})\right]\end{aligned}类似地我们可以将q^*(s,a)代入对应的Bellman方程(3)中:\tag{7} \begin{aligned}q^*(s,a) &= \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \sum_{a^{\prime}}\pi^*(a^{\prime} \mid s^{\prime})q^*(s^{\prime},a^{\prime})\right] \\ &= \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \max_{a^{\prime}}q^*(s^{\prime},a^{\prime})\right]\end{aligned}最优策略可以写为如下形式:\tag{8} \large{\pi^*(s)=\argmax_{a}q^*(s,a)}=\argmax_a\sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v^*(s^{\prime})\right]若有多个动作a都能达到q^*(s,a)的最大值,也可以将最优策略\pi^*写成随机策略的形式,即在这些使q^*(s,a)达到最大值的动作里面随机地选取一个动作。
动态规划
这一部分介绍求解强化学习问题的一类最基本的算法:动态规划 (Dynamic Programming),这类算法假设智能体事先知道马尔科夫决策过程(MDP)的所有信息,即状态转换概率p(s^{\prime},r\mid s,a),而不需要从与环境的交互中逐渐学习。我们可以利用动态规划算法首先解决以下两个问题:
- 策略评估 (Policy Evaluation):参照公式(2),给定策略\pi,计算对应的state-value function v_{\pi}(s),计算流程如下方左图所示
- 策略优化 (Policy Improvement):参照公式(1)和公式(4),给定v_{\pi}(s),可以计算出q_{\pi}(s,a)以及新的策略\pi^{\prime},满足\pi^{\prime}\ge\pi,计算流程如下方右图所示

结合上述两种算法,若有初始策略\pi,可以先通过Policy Evaluation计算出v_{\pi}(s),再通过Policy Improvement得到优化后的策略\pi^{\prime};不断重复这个过程直到\pi^{\prime}=\pi,此时策略\pi^{\prime}满足公式(8),即为最优策略\pi^*。这个方法称为策略迭代 (Policy Iteration),计算流程如下方左图所示。在策略迭代过程中,每次使用Policy Evaluation计算v_{\pi}(s)时也需要进行多次迭代(参见上方左图),我们可以对此进行改进,在Policy Evaluation时仅使用一次迭代,结合Policy Improvement有:\begin{cases}v_{\pi}(s) \leftarrow \sum_{a} \pi(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}(s^{\prime})\right],\space\text{ one iteration in Policy Evaluation} \\ v_{\pi^{\prime}}(s) \leftarrow \max_a q_{\pi}(s,a)=\max_a \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)[r+\gamma v_{\pi}(s^{\prime})],\space\text{ Policy Improvement, see formula (4) and (1)}\end{cases}容易看出上述过程可以合并为一个过程,即v_{\pi}(s) \leftarrow \max_{a}\sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}(s^{\prime})\right]参见公式(6),不断对这一过程进行迭代可以得到最优策略的state-value function v^*(s),然后通过Policy Improvement得到最优策略\pi^*,这种方法叫做价值迭代 (Value Iteration),具体计算流程如下方右图所示。

