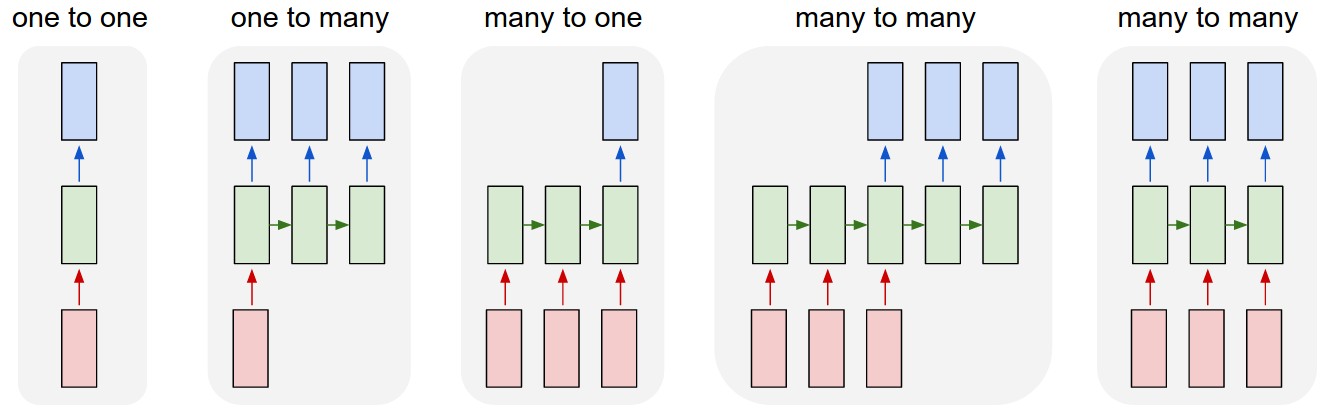
循环神经网络是用于处理序列数据的网络架构。假设输入序列的长度为T_x,输出序列的长度为T_y,则上图从左到右依次为:
- T_x=T_y=1,此时网络为普通神经网络,不包含RNN架构
- T_x=1, T_y>1,例如输入一张图片,输出对该图片的说明;或者输入一个单词,输出一段文字
- T_x>1, T_y=1,例如在情感分析中输入一段文字,输出这段文字表达的是正面情绪还是负面情绪
- T_x>1, T_y>1,序列到序列 (Seq2Seq) 模型,例如在机器翻译中输入一句英文,输出翻译后的中文
- T_x=T_y>1,输入序列和输出序列是同步的,例如在视频分类中输入一段视频,输出视频的每个帧的类别标签
不失一般性,以最右边的架构为例,RNN的基本结构可表示如下:
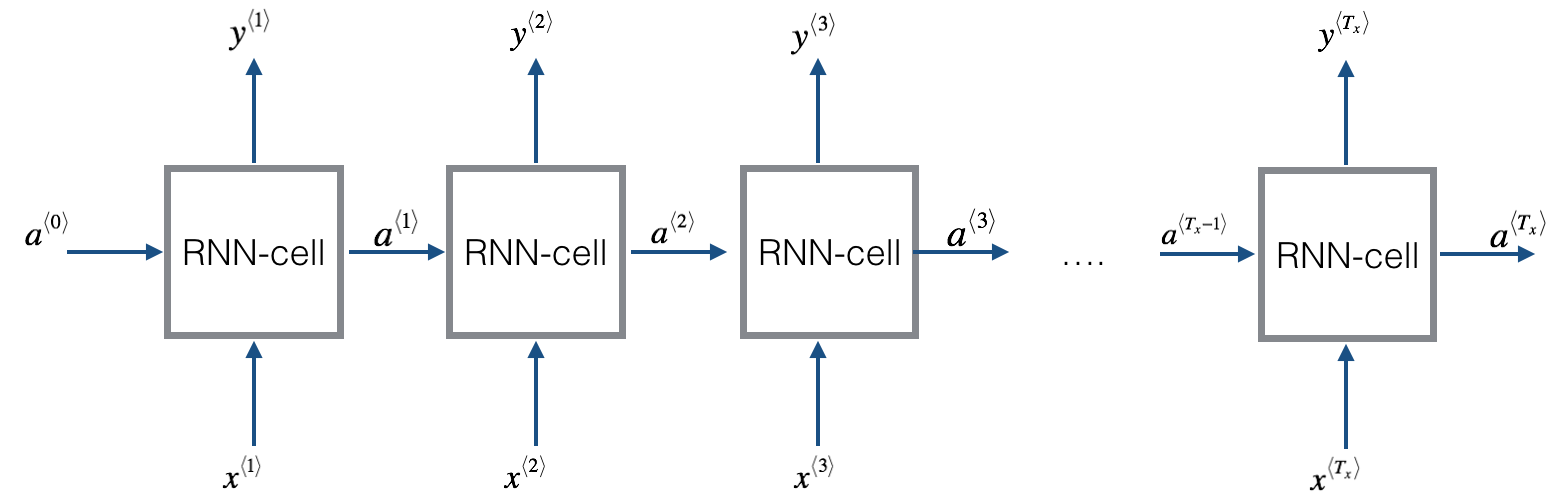
上图中的每个cell中的参数均是共享的,这也是循环一词的由来。每个cell的内部结构如下图所示:
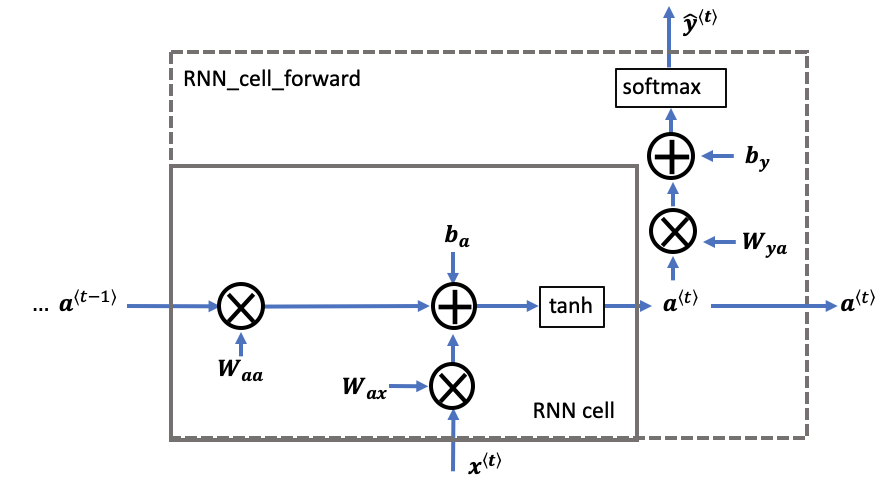
一个RNN cell中的计算公式可以表示为:\large \begin{cases}\boldsymbol{a}^{<t>}=\tanh \left({W}_{aa}\boldsymbol{a}^{<t-1>} + {W}_{ax}\boldsymbol{x}^{<t>} + {b}_{a}\right)= \tanh \left({W}_{a}[\boldsymbol{a}^{<t-1>},\space \boldsymbol{x}^{<t>}] + {b}_{a} \right) \\ \boldsymbol{\hat{y}}^{<t>}=g\left({W}_{y a} \boldsymbol{a}^{<t>}+{b}_{y}\right), \space\space g\text{为激活函数}\end{cases}其中\boldsymbol{a}^{<t>}为RNN cell的输出,\boldsymbol{\hat y}^{<t>}为RNN的预测值。在更新RNN的参数(W_a, b_a, W_{ya}, b_y)时仍使用梯度下降的方法进行计算,和普通神经网络类似,梯度仍由后向传播方法进行计算,不同的是计算过程中要考虑时间(序列步数)的因素,这种后向传播称为BPTT。这里以一个简单的情况为例进行说明:
假设T_x=3,网络损失函数等于最后一步的损失函数(记为E_3),由链式法则可以推导出参数W_{a}的梯度为\frac{\partial E_{3}}{\partial W_{a}}=\frac{\partial E_{3}}{\partial \hat{y}^{<3>}} \frac{\partial \hat{y}^{<3>}}{\partial a^{<3>}} \frac{\partial {a}^{<3>}}{\partial W_{a}} + \frac{\partial E_{3}}{\partial \hat{y}^{<3>}} \frac{\partial \hat{y}^{<3>}}{\partial a^{<3>}} \frac{\partial a^{<3>}}{\partial a^{<2>}} \frac{\partial {a}^{<2>}}{\partial W_{a}} + \frac{\partial E_{3}}{\partial \hat{y}^{<3>}} \frac{\partial \hat{y}^{<3>}}{\partial a^{<3>}} \frac{\partial a^{<3>}}{\partial a^{<2>}} \frac{\partial a^{<2>}}{\partial a^{<1>}} \frac{\partial {a}^{<1>}}{\partial W_{a}} 由上述计算容易看出步数间隔越多,在梯度计算中累乘的项数就越多,越容易出现梯度消失现象,即当前步与前面间隔较远的步之间的依赖关系在计算过程中被丢弃了,这不利于对长序列问题的处理。RNN网络的一些变种(例如LSTM、GRU)可以较好地解决梯度消失问题。
LSTM
LSTM的提出主要是为了解决RNN中的梯度消失问题,增强其对长序列问题的处理能力。如下图所示,LSTM的整体结构和RNN基本一致,不同的是RNN和LSTM中每个cell内的结构。
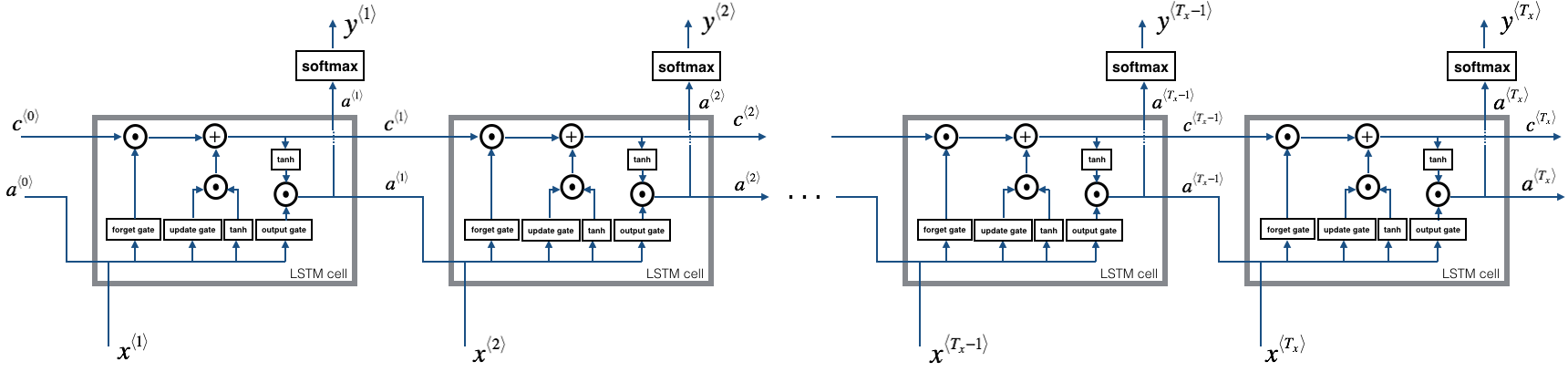
LSTM中每个cell内的结构如下图所示:
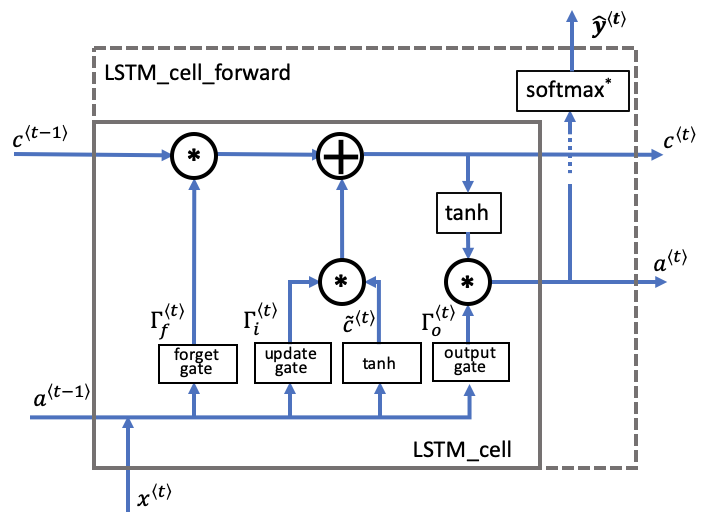
相比于RNN cell,LSTM cell中多了一个cell state,即\boldsymbol{c}^{<t>},它是在当前时间步中保留之前步的状态,增强时间步之间的依赖的关键。LSTM在cell state的计算过程中设计了两个门:
- Forget Gate: \boldsymbol{\Gamma}_{f}^{<t>}=\sigma\left({W}_{f}\left[\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{f}\right),用来控制当前的cell state有多少继承于前一时间步的cell state (即\boldsymbol{c}^{<t-1>})
- Update Gate: \boldsymbol{\Gamma}_{i}^{<t>}=\sigma\left({W}_{i}\left[\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{i}\right),用来控制当前的cell state有多少来自于当前时间步的更新 (即\boldsymbol{\tilde c}^{<t>})
当前时间步的更新\boldsymbol{\tilde c}^{<t>}=\tanh\left({W}_{c}\left[\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{c}\right),当前时间步的cell state可写为\large \boldsymbol{c}^{<t>}=\boldsymbol{\Gamma}_{f}^{<t>}*\boldsymbol{c}^{<t-1>}+\boldsymbol{\Gamma}_{i}^{<t>}*\boldsymbol{\tilde c}^{<t>}
在LSTM中还设计了一个门用于控制cell的输出:
- Output Gate: \boldsymbol{\Gamma}_{o}^{<t>}=\sigma\left({W}_{o}\left[\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{o}\right)
LSTM cell的输出为\boldsymbol{a}^{<t>}=\boldsymbol{\Gamma}_{o}^{<t>}*\tanh(\boldsymbol{c}^{<t>})
同RNN相同,LSTM的预测值可写为\boldsymbol{\hat{y}}^{<t>}=g\left({W}_{y a} \boldsymbol{a}^{<t>}+{b}_{y}\right)
类似LSTM,RNN的另一变体GRU也能较好地处理长序列问题,它的基本思想和LSTM是一致的,只是在门的设置上有所不同,这里仅列出GRU的公式,就不再详细介绍了:
- \boldsymbol{\Gamma}_{u}^{<t>}=\sigma\left({W}_{u}\left[\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{u}\right)
- \boldsymbol{\Gamma}_{r}^{<t>}=\sigma\left({W}_{r}\left[\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{r}\right)
- \boldsymbol{\tilde a}^{<t>}=\tanh\left({W}_{a}\left[\boldsymbol{\Gamma}_{r}^{<t>}*\boldsymbol{a}^{<t-1>}, \space \boldsymbol{x}^{<t>}\right]+{b}_{a}\right)
- \boldsymbol{a}^{<t>}=(1-\boldsymbol{\Gamma}_{u}^{<t>})*\boldsymbol{a}^{<t-1>}+\boldsymbol{\Gamma}_{u}^{<t>}*\boldsymbol{\tilde a}^{<t>}
Bidirectional RNN
上文介绍的RNN和LSTM的结构均为单向的,即当前时间步的预测仅依赖于该步及该步之前的输入。但是在许多应用中,特别是在自然语言处理中,当前步的预测还依赖于该步之后的输入,Bidirectional RNN可以较好地解决这类问题,它的结构如下图所示(假设T_x=T_y=4):
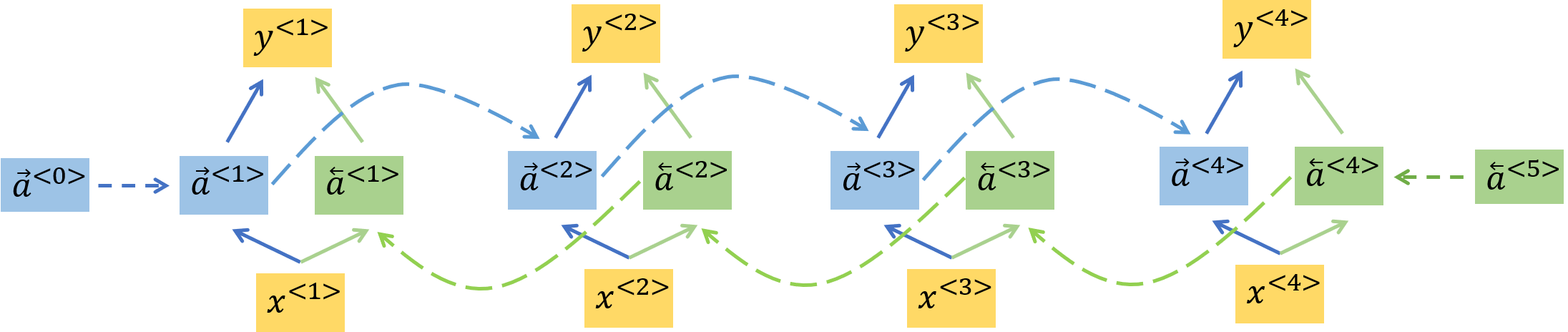
其中蓝色和绿色方块分别表示正向和反向的RNN cell,它们的计算公式为\large \begin{cases}\boldsymbol{\overrightarrow a}^{<t>}=\tanh \left({W}_{a}^{(f)}\left[\boldsymbol{\overrightarrow a}^{<t-1>},\space \boldsymbol{x}^{<t>}\right] + {b}_{a}^{(f)} \right) \\ \\ \boldsymbol{\overleftarrow a}^{<t>}=\tanh \left({W}_{a}^{(b)}\left[\boldsymbol{\overleftarrow a}^{<t+1>},\space \boldsymbol{x}^{<t>}\right] + {b}_{a}^{(b)} \right)\end{cases}Bidirectional RNN的预测值为\large \boldsymbol{\hat y}^{<t>}=g\left(W_{ya}\left[\boldsymbol{\overrightarrow a}^{<t>},\space \boldsymbol{\overleftarrow a}^{<t>}\right]+b_y\right)将RNN cell替换为LSTM cell即为Bidirectional LSTM。
