神经网络结构如下图所示:
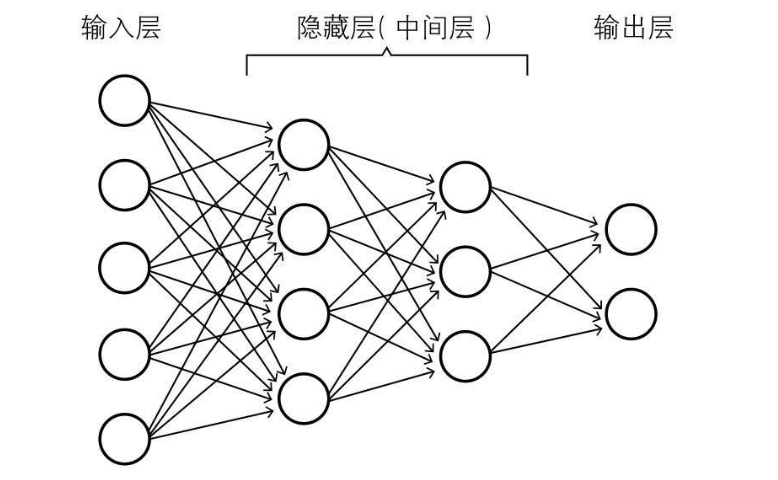
一、算法推导
关于神经网络基础的介绍已经有很多资料可以参考,但是针对其算法的推导过程多以回归问题或者二分类问题为例,即始终假设激活函数仅与当前要激活的网络节点有关。本文这部分以多分类问题为例,探讨当激活函数与对应的整个网络层都有关时算法的推导过程。首先定义一些网络架构的参数方便后续推导:
- 训练数据共有m个,训练数据集可由矩阵X=\large{\begin{bmatrix}\begin{smallmatrix} \vec{x}^{(1)} \\ \vec{x}^{(2)} \\ \vdots \\ \vec{x}^{(m)} \end{smallmatrix}\end{bmatrix}}表示,X为m行p列的矩阵(p为特征数)
- 从输入层到输出层依次记为第0,1,2,...,L层,每层的节点数记为n_0,n_1,n_2,...,n_L,可以看出n_0=p
- 第l层(l=1,2,...,L)的权重W^{[l]}为n_{l-1}行n_{l}列的矩阵,b^{[l]}为1行n_l列的矩阵
- 第l层(l=1,2,...,L)使用激活函数前的值Z^{[l]}为m行n_l列的矩阵
- 第l层(l=1,2,...,L-1)使用激活函数后的值A^{[l]}为m行n_l列的矩阵。这里假设激活函数仅为当前节点的函数,记为g(z),即 A^{[l]}_{ij}=g(Z^{[l]}_{ij}),写成矩阵形式为 A^{[l]}=g(Z^{[l]})
- 输出层(即第L层)使用激活函数后的值A^{[L]}为m行n_L列的矩阵。这里以多分类问题为例,采用softmax激活函数,激活函数记为\large g_L(z_1,z_2,\cdots,z_{n_L})=[f_1,f_2,\cdots,f_{n_L}]=\left[\frac{e^{z_1}}{\sum_{i=1}^{n_L} e^{z_i}}, \frac{e^{z_2}}{\sum_{i=1}^{n_L} e^{z_i}}, \cdots, \frac{e^{z_{n_L}}}{\sum_{i=1}^{n_L} e^{z_i}}\right]此时A^{[L]}=g_L(Z^{[L]})表示为如下形式 \large A^{[L]}_{i1}, A^{[L]}_{i2}, \cdots, A^{[L]}_{i,n_L}=g_L(Z^{[L]}_{i1}, Z^{[L]}_{i2}, \cdots, Z^{[L]}_{i,n_L})\text{, }\space\space i=1,2,\cdots,m
- 损失函数可写为\mathcal{J}=\large -\frac{1}{m}\sum\limits_{i = 1}^m\sum\limits_{j=1}^{n_L}\vec y^{(i)}_j\ln A^{[L]}_{ij},其中\vec y^{(i)}为第i个样本的真实值
1. 前向传播
- \text{for }\space\space l=1,2,\cdots,L\space :
- 线性部分: Z^{[l]} = A^{[l-1]}\cdot W^{[l]} + \underbrace{(1,1, \cdots,1)^T}_{ m}\cdot b^{[l]},其中\large \cdot表示矩阵乘法,上标T表示矩阵转置,并且A^{[0]}=X
- 非线性部分: A^{[l]}=g(Z^{[l]})
2. 后向传播
- 记dA^{[l]}为损失函数对激活后的神经网络节点的导数(l=1,2,...,L),dA^{[l]}为与A^{[l]}相同维数的矩阵,并且dA^{[l]}_{ij}=\large{\frac{\partial \mathcal{J}}{\partial A^{[l]}_{ij}}}
- 记dZ^{[l]}为损失函数对激活前的神经网络节点的导数(l=1,2,...,L),dZ^{[l]}为与Z^{[l]}相同维数的矩阵,并且dZ^{[l]}_{ij}=\large{\frac{\partial \mathcal{J}}{\partial Z^{[l]}_{ij}}}
- 记dW^{[l]}和db^{[l]}为损失函数对权重系数的导数(l=1,2,...,L),dW^{[l]}和db^{[l]}为与W^{[l]}和b^{[l]}相同维数的矩阵,并且dW^{[l]}_{ij}=\large{\frac{\partial \mathcal{J}}{\partial W^{[l]}_{ij}}}以及db^{[l]}_{1j}=\large{\frac{\partial \mathcal{J}}{\partial b^{[l]}_{1j}}}
- 记g'(Z^{[l]})为激活函数的导数(l=1,2,...,L-1),它仍为一个m行n_l列的矩阵,满足g'(Z^{[l]})_{ij}=\large \frac{dg}{dz}|_{z=Z^{[l]}_{ij}}
- 定义矩阵\triangledown g_L为如下形式:\large \triangledown g_L=\begin{pmatrix}\frac{\partial f_1}{\partial z_1} & \frac{\partial f_1}{\partial z_2} & \cdots & \frac{\partial f_1}{\partial z_{n_L}}\\ \frac{\partial f_2}{\partial z_1} & \frac{\partial f_2}{\partial z_2} & \cdots & \frac{\partial f_2}{\partial z_{n_L}} \\ \vdots \\ \frac{\partial f_{n_L}}{\partial z_1} & \frac{\partial f_{n_L}}{\partial z_2} & \cdots & \frac{\partial f_{n_L}}{\partial z_{n_L}}\end{pmatrix}根据损失函数\mathcal J容易计算出dA^{[L]},此时dZ^{[L]}的形式为\large (dZ^{[L]}_{i1},dZ^{[L]}_{i2},\cdots,dZ^{[L]}_{i,n_L})=(dA^{[L]}_{i1},dA^{[L]}_{i2},\cdots,dA^{[L]}_{i,n_L})\cdot\triangledown g_L|_{z_1,z_2,\cdots,z_{n_L}=Z^{[L]}_{i1},Z^{[L]}_{i2},\cdots,Z^{[L]}_{i,n_L}}其中i=1,2,\cdots,m
后向传播的计算过程可表示为:
- \text{for}\space\space l=L,L-1,\cdots,1\space :
- db^{[l]} = \large \frac{\partial \mathcal{J} }{\partial b^{[l]}} \normalsize =\sum_{i=1}^m dZ^{[l]}_{i\bold{\_}} = \underbrace{(1,1,\cdots,1)}_{m}\cdot dZ^{[l]}
- dW^{[l]} = \large \frac{\partial \mathcal{J} }{\partial W^{[l]}} \normalsize = A^{[l-1] T}\cdot dZ^{[l]}
- \text{if}\space\space l\gt 1\space :
- dA^{[l-1]} = \large \frac{\partial \mathcal{J} }{\partial A^{[l-1]}} \normalsize = dZ^{[l]} \cdot W^{[l] T}
- dZ^{[l-1]}=\large \frac{\partial \mathcal{J} }{\partial Z^{[l-1]}} \normalsize =dA^{[l-1]}* g'(Z^{[l-1]}),其中*表示矩阵的每个元素相乘
3. 参数更新
采用梯度下降法对权重系数进行更新
- \text{for }\space\space l=1,2,\cdots,L\space :
- W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]}以及b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]},其中\alpha为学习率
二、应用技巧
1. 对输入X进行归一化,将每个特征的均值变为0,方差变为1
2. 为减轻梯度消失/爆炸问题,需对W^{[l]}进行合适的初始化,常用的初始化方法如下表所示:
| 激活函数g(z) | 从Uniform(-r, r)中抽样 | 从Normal(0,\sigma^2)中抽样 | 方法的参考文献 |
| tanh | \large r=\sqrt{\frac{\large 3}{\large (n_{l-1}+n_l)/2}} | \large \sigma=\sqrt{\frac{\large 1}{\large (n_{l-1}+n_l)/2}} | Xavier(Glorot) Initialization |
| ReLU (and its variants) | \large r= \sqrt{\frac{\large 6}{\large n_{l-1}}} | \large \sigma=\sqrt{\frac{\large 2}{\large n_{l-1}}} | He Initialization |
Keras中的实现:
- Xavier(Glorot) Initialization: tensorflow.keras.initializers.VarianceScaling(scale=1.0, mode="fan_avg", distribution=... )
- He Initialization: tensorflow.keras.initializers.VarianceScaling(scale=2.0, mode="fan_in", distribution=...)
3. 隐藏层的激活函数g(z)常选用ReLU或者其变种,这里列举常用的三个:
- ReLU: \large g(z)=\max (0,z)
- Leaky ReLU: \large g(z)=\max (0,z) + \min (0, \alpha z),其中\alpha为一个正的常数,例如0.01
- ELU: \large g(z)=\max (0,z) + \min \left( 0, \alpha (e^z-1) \right),其中\alpha为一个正的常数,例如1
4. 为减少训练过程中的过拟合,可使用以下几种方法:
L2 Regularization (Weight Decay):仍以多分类问题为例,此时的损失函数变为\large \mathcal{J}=-\frac{1}{m}\sum\limits_{i = 1}^m\sum\limits_{j=1}^{n_L}\vec y^{(i)}_j\ln A^{[L]}_{ij}+\underbrace{\frac{\lambda}{2} \sum\limits_{l=1}^{L}\sum\limits_{k=1}^{n_{l-1}}\sum\limits_{j=1}^{n_l} \left(W_{kj}^{[l]}\right)^2 }_\text{L2 regularization cost}
Dropout:在每次训练过程中随机关掉神经网络中的一些节点,对矩阵A^{[l]},有对应的开关矩阵D^{[l]},生成D^{[l]}的代码为
|
1 2 |
Dl = np.random.rand(Al.shape[0], Al.shape[1]) #Step 1: initialize matrix D1 = np.random.rand(..., ...) Dl = (Dl<keep_prob) #Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold) |
此时神经网络的前向传播和后向传播也要进行额外处理:
- 在前向传播过程中按文章第一部分中的公式计算出A^{[l]}后:\large A^{[l]}=A^{[l]}*D^{[l]}\text{, }\space\space A^{[l]}=A^{[l]}/keep\_prob
- 在后向传播过程中使用上步计算的A^{[l]}进行计算,并且按文章第一部分中的公式计算出dA^{[l]}后:\large dA^{[l]}=dA^{[l]}*D^{[l]}\text{, }\space\space dA^{[l]}=dA^{[l]}/keep\_prob
- 需要注意的是在使用训练好的网络进行验证或预测时不要使用Dropout(即将keep\_prob设为1)
5. 为减少训练过程中不必要的震荡,加快收敛速度,并且尽可能地避免落入局部最优值,有一些改进的梯度下降算法可用来代替原始的梯度下降算法:
\large \text{Momentum: }\space\space\begin{cases}v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta) dW^{[l]} \\W^{[l]} = W^{[l]} - \alpha v_{dW^{[l]}}\end{cases}\text{ and }\begin{cases}v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta) db^{[l]} \\b^{[l]} = b^{[l]} - \alpha v_{db^{[l]}}\end{cases}\large \text{RMSProp: }\space\space\begin{cases}s_{dW^{[l]}} = \beta s_{dW^{[l]}} + (1 - \beta) {dW^{[l]}*dW^{[l]}} \\ W^{[l]} = W^{[l]} - \alpha\frac{\large dW^{[l]}}{\large \sqrt{s_{dW^{[l]}}} + \epsilon}\end{cases}\text{ and }\begin{cases}s_{db^{[l]}} = \beta s_{db^{[l]}} + (1 - \beta){db^{[l]}*db^{[l]}} \\b^{[l]} = b^{[l]} - \alpha\frac{\large db^{[l]}}{\large \sqrt{s_{db^{[l]}}} + \epsilon}\end{cases}
\large \text{Adam: }\space\space\begin{cases}v_{dW^{[l]}} = \beta_1 v_{dW^{[l]}} + (1 - \beta_1) dW^{[l]} \\ v^{corrected}_{dW^{[l]}} = \frac{\large v_{dW^{[l]}}}{\large 1 - (\beta_1)^t} \\ \\ s_{dW^{[l]}} = \beta_2 s_{dW^{[l]}} + (1 - \beta_2) {dW^{[l]}*dW^{[l]}} \\ s^{corrected}_{dW^{[l]}} = \frac{\large s_{dW^{[l]}}}{\large 1 - (\beta_2)^t} \\ \\ W^{[l]} = W^{[l]} - \alpha \frac{\large v^{corrected}_{dW^{[l]}}}{\large \sqrt{s^{corrected}_{dW^{[l]}}} + \epsilon}\end{cases}\text{ and }\begin{cases}v_{db^{[l]}} = \beta_1 v_{db^{[l]}} + (1 - \beta_1) db^{[l]} \\ v^{corrected}_{db^{[l]}} = \frac{\large v_{db^{[l]}}}{\large 1 - (\beta_1)^t} \\ \\s_{db^{[l]}} = \beta_2 s_{db^{[l]}} + (1 - \beta_2) {db^{[l]}*db^{[l]}} \\ s^{corrected}_{db^{[l]}} = \frac{\large s_{db^{[l]}}}{\large 1 - (\beta_2)^t} \\ \\ b^{[l]} = b^{[l]} - \alpha \frac{\large v^{corrected}_{db^{[l]}}}{\large \sqrt{s^{corrected}_{db^{[l]}}} + \epsilon}\end{cases}\text{Adam}方法中的t代表迭代次数(即参数更新的次数)
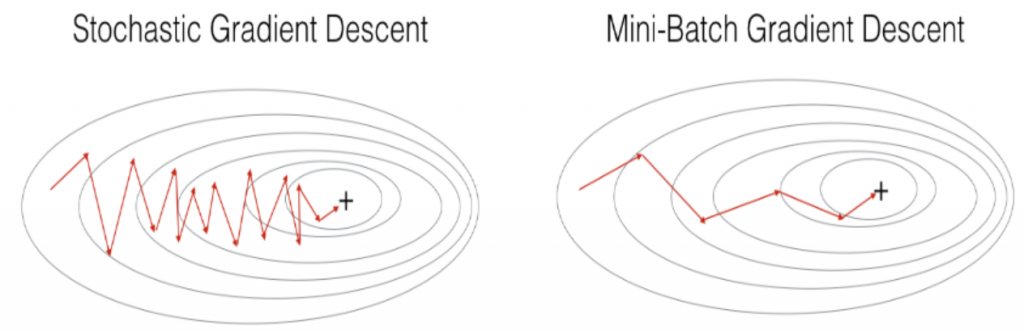
6. 在第一部分的算法推导中可以看到使用梯度下降进行一次参数更新需使用全部m个训练样本,计算效率较低,并且容易陷入局部最优值;随机梯度下降一次更新仅使用一个训练样本,但在过程中会产生较剧烈的震荡,影响最终的优化结果;Mini-Batch梯度下降则介于梯度下降和随机梯度下降两者之间,一次更新使用部分样本(记为一个batch)。若选取合适大小的batch (例如32,64,128),Mini-Batch梯度下降常优于梯度下降和随机梯度下降。
7. 学习率\alpha可以是常数,也可以根据训练进度而变化,常用的几种方法有:
- Learning Rate Decay: \alpha = {\alpha_0}/(1+d*e),其中d表示衰减率,\alpha_0表示初始学习率,e表示训练的轮数,迭代次数(即参数更新的次数)等于e*m/bz,bz为每次迭代使用的训练样本个数(即一个batch的大小)
- Cyclic Learning Rate:如下图所示,横坐标表示迭代次数
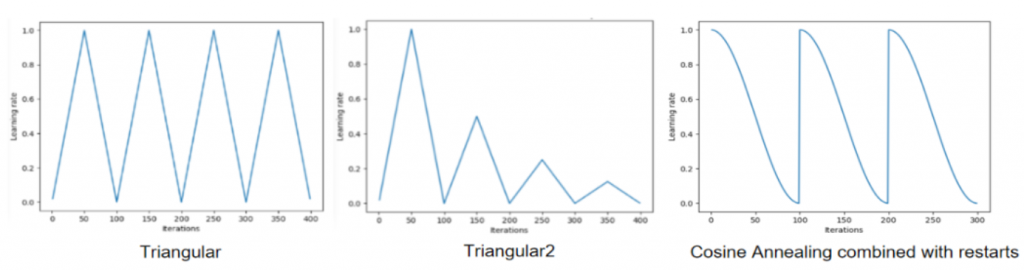
8. 神经网络在训练过程中经常会出现Internal Covariate Shift,即每层的输出的分布会随着参数的更新不断变化,而每层的输出又是后续层的输入,导致按照之前的输入分布训练得到的参数需要重新适应新的分布,这就降低了神经网络的训练效率,使之不容易收敛。为解决这一问题,可以使用Batch Normalization这一技术。
Batch Normalization通常和Mini-Batch梯度下降一起使用,因此不同于文章第一部分,这里的Z^{[l]}为bz行n_l列的矩阵,bz为一个batch的大小,即每次参数更新使用的训练样本数量。这里以第l层网络的第j个节点(j=1,2,\cdots,n_l)为例进行说明,Batch Normalization的计算过程如下:
- 计算节点的均值:\large \mu_j = \frac{1}{bz}\sum_{i=1}^{bz}Z^{[l]}_{ij}
- 计算节点的方差:\large \sigma^2_j = \frac{1}{bz}\sum_{i=1}^{bz}(Z^{[l]}_{ij}-\mu_j)^2
- 调整节点的均值和方差:\large Z^{[l]}_{ij}=\gamma_j\frac{\large Z^{[l]}_{ij}-\mu_j}{\large \sqrt{\sigma^2_j+\epsilon}}+\beta_j,其中\gamma_j和\beta_j为需要训练的参数,i=1,2,\cdots,bz
- 在使用训练好的网络进行验证或预测时需用总体的均值\hat{\mu}_j和方差\hat{\sigma}^2_j代替每个batch的均值和方差,总体的均值和方差由训练时每次迭代使用的batch的均值和方差不断进行更新得到:\large \hat{\mu}_j=\tau\hat{\mu}_j+(1-\tau)\mu_j\space\text{ and }\space \hat{\sigma}^2_j=\tau\hat{\sigma}^2_j+(1-\tau)\sigma^2_j
上述步骤是在Z^{[l]}上(即在激活函数之前)使用Batch Normalization,也有研究证明在A^{[l]}上(即在激活函数之后)使用Batch Normalization也可以产生较好的效果。
